
Devoir maison sur les fonction a remttre dans 10h
10 messages
- Page 1 sur 1
Re: Devoir maison sur les fonction a remttre dans 10h (URGEN
Déjà, dire bonjour ne coûte rien et c'est un minimum de politesse. Ensuite, si tu avais lu le règlement du forum, tu saurais que les "DM", "devoir maison", "besoin d'aide", "urgent", "aidez-moi" etc sont interdits. Tu aurais pu dire ce que tu as fait, ce que tu as tenté, où tu bloques, bref où sont tes problèmes. Je ne parle même pas du fait de s'y prendre 10h avant de devoir le rendre et surtout à 3h du matin, je ne suis pas sûr que ce soit le meilleur horaire pour espérer de l'aide... Je tiens à mettre les choses au clair, tu es ici sur un forum d'entraide, le but est d'aider, n'espère pas que quelqu'un fasse tes devoirs à ta place. Pour finir, il est inutile de poster plusieurs fois la même discussion en espérant que cela te permette d'obtenir une réponse plus rapidement, il est 3h du matin : s'il n'y a pas grand monde pour y répondre, ça ne va pas les réveiller. En plus, ça pollue le forum et tu n'es pas seul à avoir besoin d'aide. 
Du coup, j'attends que tu nous dises ce que tu as fait : là où tu as su faire et là où tu bloques. Sans un minimum de détails de ta part, ce sera difficile de savoir où et comment t'aider.

Du coup, j'attends que tu nous dises ce que tu as fait : là où tu as su faire et là où tu bloques. Sans un minimum de détails de ta part, ce sera difficile de savoir où et comment t'aider.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Devoir maison sur les fonction a remttre dans 10h (URGEN
Excusez moi de mon impolitesse , Bonjour enfaites si j'ai posté l'exercices entier c'est parce'que je ne comprend rien dans les maths , ma professeur a dit de se débrouiller pour rattrappé toute les lacunes que j'ai accumulé car elle ne vas pas refaire les bases pour moi seulement . Je suis allé sur youtube mais je ne comprend pas trop car il y a plus de chiffre alors que sur la vidéo cela est plus facile .
Re: Devoir maison sur les fonction a remttre dans 10h (URGEN
Ok. Pas de soucis, mais la prochaine fois je te conseille de t'y prendre plus tôt. A cet heure-ci je doute que tu reçoive beaucoup d'aide. Bref commençons.
Pour l'exercice 1 :
1. Calculer l'image d'une réel quelconque par
par  , c'est calculer
, c'est calculer ) en remplaçant
en remplaçant  par le réel
par le réel  en question. Par exemple, si
en question. Par exemple, si =x^2) , l'image de
, l'image de 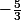 par
par  est
est = \left( - \frac 5 3\right)^2 = \frac{5^2}{3^2} = \frac{125}{9}) .
.
2. Trouver les antécédents de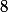 par
par  revient à chercher tous les réels
revient à chercher tous les réels  dont l'image
dont l'image ) par
par  soit égale à
soit égale à 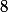 , c'est-à-dire qu'il faut trouver tous les réels
, c'est-à-dire qu'il faut trouver tous les réels  solution de l'équation
solution de l'équation =8) . Mais
. Mais =x^2) donc il faut résoudre
donc il faut résoudre 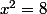 .
.
3. Dit autrement, on a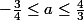 . Encadrer un réel
. Encadrer un réel  , c'est trouver deux autres réels
, c'est trouver deux autres réels  et
et  tels que l'on ait
tels que l'on ait 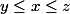 (
( est encadré par
est encadré par  et
et  ). Or d'après le cours, les variations de la fonction
). Or d'après le cours, les variations de la fonction  t'indiquent qu'il faut séparer l'encadrement de
t'indiquent qu'il faut séparer l'encadrement de  en deux cas suivant que
en deux cas suivant que 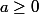 ou
ou 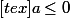 [/tex].
[/tex].
Premier cas : Si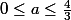 alors
alors 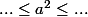 ;
;
Deuxième cas : si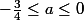 alors
alors 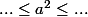 .
.
Déduis-en alors un encadrement de lorsque
lorsque 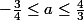 .
.

Pour l'exercice 1 :
1. Calculer l'image d'une réel quelconque
2. Trouver les antécédents de
3. Dit autrement, on a
Premier cas : Si
Deuxième cas : si
Déduis-en alors un encadrement de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Devoir maison sur les fonction a remttre dans 10h (URGEN
Salut,
Pas du tout responsable de ta part de commencer un devoir à 3h du mat et le rendre le matin même ...
Capitaine t'a déjà fournit des indices pour le 1/
Pour le 2 :
1- Utilise\times(c+d) = ac + ad + bc + bd) avec
avec 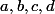 des nombres quelconques réels et en particuler
des nombres quelconques réels et en particuler ^2 = a^2 -2ab + b^2)
2- Remarque que = (-2+x)) est facteur commun.
est facteur commun.
3 - il suffit que tu développes l'expression en utilisant mon deuxième indice en 2/1- en remplaçant le par
par 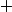 .
.
Pour le 3 :
Calcule la valeur de la fonction par pas de 0.25 en abscisse pour la partie droite (x positif) du graphique. Comme la fonction est paire, il faudra donc prendre le symétrique par rapport à l'axe des ordonnées pour chaque point à droite.
Pas du tout responsable de ta part de commencer un devoir à 3h du mat et le rendre le matin même ...
Capitaine t'a déjà fournit des indices pour le 1/
Pour le 2 :
1- Utilise
2- Remarque que
3 - il suffit que tu développes l'expression en utilisant mon deuxième indice en 2/1- en remplaçant le
Pour le 3 :
Calcule la valeur de la fonction par pas de 0.25 en abscisse pour la partie droite (x positif) du graphique. Comme la fonction est paire, il faudra donc prendre le symétrique par rapport à l'axe des ordonnées pour chaque point à droite.
Re: Devoir maison sur les fonction a remttre dans 10h (URGEN
Edit : un pas de 0.5 fait finalement l'affaire vu l'échelle du graphique
Re: Devoir maison sur les fonction a remttre dans 10h (URGEN
Pour l'exercice 2 :
1. Développer et réduire l'expression) signifie effectuer les opération qu'il est possible de faire.
signifie effectuer les opération qu'il est possible de faire.
Ici par exemple, tu as un premier produit(3-5x)) , il faut donc le développer. Cela donne
, il faut donc le développer. Cela donne (3-5x) = x(3-5x)-2(3-5x) = 3x-5x^2-6+10x) . Puis on réduit : il y a deux termes en "
. Puis on réduit : il y a deux termes en " " donc :
" donc : 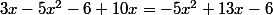 . On a développé et réduis le produit
. On a développé et réduis le produit (3-5x)) , cela donne
, cela donne 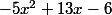 .
.
Fais-en de même pour le second produit^2) .
.
Il est possible qu'une fois le développement-réduction de^2) obtenu, il faille encore réduire !
obtenu, il faille encore réduire !
2. Factoriser une expression, c'est l'exprimer uniquement comme des produits. Ici, remarque que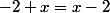 est un "facteur" commun de
est un "facteur" commun de (3-5x)) et
et ^2) , donc en écrivant que
, donc en écrivant que ^2=(x-2)(...)) , tu as
, tu as =(x-2)( (3-5x) +(...) )) .
.
3. Développe et réduis l'expression^2 + \frac {49} 4) donnée par le sujet. Tu devrais retomber sur la même expression que dans la question 1. D'où l'égalité à montrer.
donnée par le sujet. Tu devrais retomber sur la même expression que dans la question 1. D'où l'égalité à montrer.
1. Développer et réduire l'expression
Ici par exemple, tu as un premier produit
Fais-en de même pour le second produit
Il est possible qu'une fois le développement-réduction de
2. Factoriser une expression, c'est l'exprimer uniquement comme des produits. Ici, remarque que
3. Développe et réduis l'expression
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Devoir maison sur les fonction a remttre dans 10h (URGEN
merci a vous tous de m'avoir soutenue sa ma bien aidé maintenant je suis a l"exo 3 mais je suis coincé
Re: Devoir maison sur les fonction a remttre dans 10h (URGEN
Pour l'exercice 3 il faut construire quelques points puis relier la courbe.
Tu sais que la courbe est composé des points de la forme (x,f(x)).
Pour x = 2 on a f(2)=2^2 = 4. Donc le point (2,4) appartient à la courbe.
De la même manière complète :
f(0) = ... donc le point (0,...) appartient à la courbe
f(1) = ... donc le point (1,...) appartient à la courbe
f(3) = ... donc le point (3,...) appartient à la courbe
f(-1) = ... donc le point (-1,...) appartient à la courbe
f(-2) = ... donc le point (-2,...) appartient à la courbe
f(-3) = ... donc le point (-3,...) appartient à la courbe
Y'a plus qu'à tracer !
Tu sais que la courbe est composé des points de la forme (x,f(x)).
Pour x = 2 on a f(2)=2^2 = 4. Donc le point (2,4) appartient à la courbe.
De la même manière complète :
f(0) = ... donc le point (0,...) appartient à la courbe
f(1) = ... donc le point (1,...) appartient à la courbe
f(3) = ... donc le point (3,...) appartient à la courbe
f(-1) = ... donc le point (-1,...) appartient à la courbe
f(-2) = ... donc le point (-2,...) appartient à la courbe
f(-3) = ... donc le point (-3,...) appartient à la courbe
Y'a plus qu'à tracer !
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Devoir maison sur les fonction a remttre dans 10h (URGEN
De rien 
Tu peux déjà tracer les points à coordonnées entière. Il y a 7 entiers dans l'intervalle [-3,3], trouve l'image de chacun d'eux. Après essaie de suivre ce que Yezu a dit.
Edit : grillé par Sylviel
Tu peux déjà tracer les points à coordonnées entière. Il y a 7 entiers dans l'intervalle [-3,3], trouve l'image de chacun d'eux. Après essaie de suivre ce que Yezu a dit.
Edit : grillé par Sylviel
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
