Bonjours, j'aurrais besoins d'aide pour un devoir s'il vous plait...
Le premier exercice est le suivant:
Les suites (Un) et (Vn) sont définie pour tout nombre naturel n par:
Un=n^2 et Vn= 2n+1/n+3
1) Vérifiez que les deux suites sont bien strictement croissante.
J'ai fais pour Un et j'ai commencé Vn:
Un: n^2
f(x)=x^2=n^2=Un
f(x) est croissante sur [0;+l'infinie[
Donc
Un est strictement croissante.
Vn=2n+1/n+3
V(n+1)=2(n+1)+1/(n+1)+3
=2(n+1)+1/n+4
U(n+1)-Un
2(n+1)+1/n+4 - 2n+1/n+3
Et a partir de la je bloque...
2) prouvez qu'a partir d'un certain entier m, que vous préciserez , tous les termes d'indice n de la suite(Un), avec n>= m , sont dzns l'intervalle I=[10 000;+infinie[.
3) Prouvez qu3 tous les termes de la suite (Vn) sont inférieur à 2.
Devoir maison de mathématique sur les suites numériques
4 messages
- Page 1 sur 1
Re: Devoir maison de mathématique sur les suites numériques
Sayachan a écrit:
La suite (Vn) sont définie pour tout nombre naturel n par:
Vn= 2n+1/n+3
Vn=2n+1/n+3
si c'est
Vn=(2n+1)/(n+3)
ce que tu as écrit signifie
Re: Devoir maison de mathématique sur les suites numériques
Ah excuse moi....c'est (2(n+1)+1)/((n+1)+3)
Re: Devoir maison de mathématique sur les suites numériques
Pour la monotonie de ) , il suffit de mettre au même dénominateur dans l'expression de
, il suffit de mettre au même dénominateur dans l'expression de 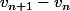
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 118 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
