Devoir maison fonction

par **Damien42530** » 25 Oct 2013, 10:08

ampholyte a écrit:Pour x 1 il faut que tu prouves que :

Même principe que l'autre question, tu dois mettre au carré chaque côté de l'inégalité.

Pour x< 1

par **ampholyte** » 25 Oct 2013, 10:10

Tu as oublié le moins sur la gauche, tu devrais trouver

par **Damien42530** » 25 Oct 2013, 10:12

ampholyte a écrit:Tu as oublié le moins sur la gauche, tu devrais trouver

Ou sa ? je n'est pas compris ton dernier message

par **ampholyte** » 25 Oct 2013, 10:14

par **Damien42530** » 25 Oct 2013, 10:18

ampholyte a écrit:

A oui ok merci et j'ai semblement a faire sa et c'est prouvé ?

Donc :

par **ampholyte** » 25 Oct 2013, 10:31

Et bien, tu dois encore simplifier (par exemple en supprimant les x) et en essayant d'obtenir une forme qui est vraie (vraie dans le sens, l'expression est vrai donc CQFD).

par **Damien42530** » 25 Oct 2013, 10:33

ampholyte a écrit:Et bien, tu dois encore simplifier (par exemple en supprimant les x) et en essayant d'obtenir une forme qui est vraie (vraie dans le sens, l'expression est vrai donc CQFD).

Comme sa ?

Donc :

par **ampholyte** » 25 Oct 2013, 10:49

C'est juste, or tu es dans le cas ou x 1 maintenant

par **Damien42530** » 25 Oct 2013, 10:54

ampholyte a écrit:C'est juste, or tu es dans le cas ou x 1 maintenant

Je l'ai fais et j'obtiens aussi

par **ampholyte** » 25 Oct 2013, 11:01

Tu as dû oublier de changer le signe de l'inégalité lorsque tu as divisé par -2 =).

par **Damien42530** » 25 Oct 2013, 11:09

ampholyte a écrit:Tu as dû oublier de changer le signe de l'inégalité lorsque tu as divisé par -2 =).

Pour x>1

Sa doit être sa non ?
Et mainetant la question est compléter ou il faut plus ? ??

par **Damien42530** » 25 Oct 2013, 11:48

ampholyte ?

par **ampholyte** » 25 Oct 2013, 12:35

C'est ok pour la question =).

par **Damien42530** » 25 Oct 2013, 14:50

ampholyte a écrit:C'est ok pour la question =).

Sa me donne que pour x>1 ---->

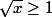
et que pour x

mais se ne montre pas que pour tout réel

Si ?

par **ampholyte** » 25 Oct 2013, 15:01

Tu as prouvé que pour 0 < x < 1 c'était vrai et que pour x > 1 c'était vrai également donc l'inégalité est pourvée =).

par **Damien42530** » 25 Oct 2013, 20:40

Voila les 5 questions de l'exercices , peux-tu me dire si tout est juste , où est-ce qu'il faut rajouter des étapes et tout sa ? Merci d'avance

Donc en Résumé :

Enoncé : Soit f définie sur [1;+infini[ par :

A) Montrer que pour tout x de [1;+infini[ ,

Donc

Comme la fonction est strictement croissante sur [1;+infini[ , je peux appliquer la fonction racine carré , qui donne :

Résolue Oui Non ???

B) Démontrer que pour tout x de [1;+infini[ ,

Donc

Résolue Oui Non ???

C) En déduire que pour tout x de [1;+infini[ ,

Donc

Résolue Oui Non ???

D) En déduire que pour tout x de

Donc

car x appartient à [1;+infini[

Résolue Oui Non ???

E) Montrer que pour tout réel

Donc pour x 1

Donc comme 0

et que pour x > 1 ---->

Alors j'en déduis que pour tout réel

Résolue Oui Non ???

Merci

Ouf enfin tout fini ^^

par **Damien42530** » 26 Oct 2013, 13:50

Quelqu'un peut m'aider ?

par **Damien42530** » 27 Oct 2013, 17:18

Personne ?

par **ampholyte** » 27 Oct 2013, 19:00

A) Ok

B) Ok

C) Petit problème. Tu n'as pas de = devant les inégalités tu pourrais dans certains cas mettre un mais pas de =.

Tu dois également préciser que comme la fonction racine est positive alors la somme de deux racines est forcément positive.

A part ça c'est ok

E) Fait le raisonnement à l'envers, je te l'ai expliqué pour que tu comprennes la démarche mais inverse simplement l'ordre.

Commence par x 2[/TEX]

etc...

Même chose pour x > 1

D) Même remarque que pour la E), inverse l'ordre de tes inéquations.

par **Damien42530** » 27 Oct 2013, 19:14

Ah ok j'ai compris je récupère ces petites erreurs .

Devoir maison fonction

Qui est en ligne