Devoir maison un exercice dérivation

[sandraj]

Changement

[Ramanujan71]

Bonjours j'ai un devoir maison à rendre pour demain , étant donné que j'ai raté quelques questions je n'arrive pas à faire mon exercice , je poste l'exercice ci dessous :

1) déterminer le nombre dérivé de la fonction f : x-> 2x-3 en a= 3 puis en a= -6
2) Que conjecture t-on ?
3) Déterminer f'(a) pour a un réel quelconque

Je ne demande pas à ce que l'on me fasse mon dm mais seulement des explications pour chaque partie , merci pour votre aide

Connais tu la dérivée de ?

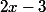
[mcar0nd]

Salut, pour la première question, il faut que tu calcule pour a=3 puis a=-6.

[sandraj]

Connais tu la dérivée de ?

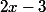
Je ne comprend vraiment pas , mais pour le petit 1) j'avais essayé de calculer a= 3 en faisant

f(3+h)
=(3+h)²
= 9+h²

f(3)= 3²
=9

f(3+h)-f(3)
=(3+h)²-3²

=(3+h+3)(3+h-3)
=h(6+h)

donc
(f(3+h)- f(3)
-----------
h

= 6+h

De un je ne sais pas du tout si c'était ce qu'il fallait faire et ensuite comment on procède quand c'est un moins ..

[mcar0nd]

Tu es bien parti, le nombre dérivée L d'une fonction f est .
Dans ton cas, , comme tu l'as dit, donc, quand h tend vers 0, le nombre dérivée vaut quoi?

[sandraj]

Tu es bien parti, le nombre dérivée L d'une fonction f est .
Dans ton cas, , comme tu l'as dit, donc, quand h tend vers 0, le nombre dérivée vaut quoi?

Il vaut 6 ?

[mcar0nd]

Il vaut 6 ?

C'est bien ça.
Maintenant, si tu fais pareil pour a=-6, tu trouves que le nombre dérivé vaut combien?

[sandraj]

C'est bien ça.
Maintenant, si tu fais pareil pour a=-6, tu trouves que le nombre dérivé vaut combien?

j'ai trouvé -12

[mcar0nd]

j'ai trouvé -12

C'est juste aussi.
Pour la question b), qu'est ce que tu peux conjecturer à propos de la dérivée de ?

[sandraj]

C'est juste aussi.
Pour la question b), qu'est ce que tu peux conjecturer à propos de la dérivée de ?

on fait 6-12 ?

= -6 ?

[mcar0nd]

on fait 6-12 ?

= -6 ?

Non. Pour a=3 tu as f'(3)=6 et pour a=-6 tu as f'(-6)=-12.
Qu'est ce que tu remarques?

[sandraj]

Non. Pour a=3 tu as f'(3)=6 et pour a=-6 tu as f'(-6)=-12.
Qu'est ce que tu remarques?

je remarque que pour f'(3) qui est égal a 6 ce sont des multiples de 2 . 3x2 = 6
-6x 2 = -12

[mcar0nd]

je remarque que pour f'(3) qui est égal a 6 ce sont des multiples de 2 . 3x2 = 6
-6x 2 = -12

C'est ça, a chaque, pour avoir f'(a), tu as multiplié par 2. Donc la dérivée de semblerait être quoi?

[sandraj]

C'est ça, a chaque, pour avoir f'(a), tu as multiplié par 2. Donc la dérivée de semblerait être quoi?

que on doit remplacer x par a

[mcar0nd]

que on doit remplacer x par a

Non, en fait, tu remarque que f'(a)=2a donc que la dérivée de serait .
Maintenant il faut le prouver, à la question c).

[sandraj]

Non, en fait, tu remarque que f'(a)=2a donc que la dérivée de serait .
Maintenant il faut le prouver, à la question c).

Donc je dois prendre n'importe qu'elle chiffre et faire comme le petit 1 pour le prouver ?

[mcar0nd]

Donc je dois prendre n'importe qu'elle chiffre et faire comme le petit 1 pour le prouver ?

Tu dois calculer sans donner de valeur a a, et ensuite, tu regarde la limite de ça quand h tend vers 0.

[sandraj]

Tu dois calculer sans donner de valeur a a, et ensuite, tu regarde la limite de ça quand h tend vers 0.

c'est à dire

f(1+h)-f(1)
_________
h

f(1+h) = ( 1+h)²

= 1+2h+ h² et f(1) = 1

f(1+h)-f(1)
=1+2h+h²-1
2h-h²(1+h)


f(1+h)-f(1)
________
h

=2+h?

Désolé si je prend du temps , j'essaie de comprendre , merci au faites de bien vouloir m'aider , j'apprécie

[mcar0nd]

Non, la tu as donné une valeur à a, ce qu'il ne faut pas faire pour trouver la dérivée de par cette méthode.
Il faut que tu calcule , mais sans donner de valeurs particulières à a. Par exemple, tu vas avoir et ainsi de suite, puis tu simplifies l'expression pour trouver la dérivée de la fonction f.

[sandraj]

Non, la tu as donné une valeur à a, ce qu'il ne faut pas faire pour trouver la dérivée de par cette méthode.
Il faut que tu calcule , mais sans donner de valeurs particulières à a. Par exemple, tu vas avoir et ainsi de suite, puis tu simplifies l'expression pour trouver la dérivée de la fonction f.

Ensuite je fais :

= (2xa + 2xh)- 3
=2 +h² - 3
= -1 +h²

f'(a) pour a un réel quelconque = -1 ?