Devoir Maison "Etudes du sens de variation d'une fonction"

[mcar0nd]

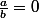
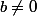
Quand tu as un quotient, tu sais que la division par 0 est strictement interdite. Donc avec donc comment tu peux faire pour que la fraction soit nulle?

[Helpme38]

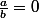
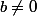
Quand tu as un quotient, tu sais que la division par 0 est strictement interdite. Donc avec donc comment tu peux faire pour que la fraction soit nulle?

je comprend pas ... :/

[mcar0nd]

je comprend pas ... :/

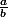
Dans une fraction , le dénominateur est toujours différent de 0 puisque tu sais que la division par zéro est interdite.
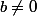
Sachant ça et que tu veux en respectant , tu ne peux avoir que .
C'est à dire que quand tu cherches les solutions d'une équation de la forme , ça revient à chercher les solutions de .

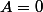
[Helpme38]

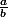
Dans une fraction , le dénominateur est toujours différent de 0 puisque tu sais que la division par zéro est interdite.
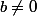
Sachant ça et que tu veux en respectant , tu ne peux avoir que .
C'est à dire que quand tu cherches les solutions d'une équation de la forme , ça revient à chercher les solutions de .

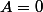
a d'accord j'ai compris donc la sa me donne 3x²+12x+9 c 'est ça ?

[mcar0nd]

a d'accord j'ai compris donc la sa me donne 3x²+12x+9 c 'est ça ?

La dérivée de ta fonction f est et tu veux , donc tu dois résoudre finalement, .

[Helpme38]

La dérivée de ta fonction f est et tu veux , donc tu dois résoudre finalement, .

3x²+12x=9
x²+x=9+3+12
3x²=24
x²= 24/3
x²=8
x=?

[mcar0nd]

3x²+12x=9
x²+x=9+3+12
3x²=24
x²= 24/3
x²=8
x=?

Oula non, tu ne peux pas faire ça.
Il faut que utilise le discriminant et le calcul des racines pour résoudre cette équation.

[Cheche]

Tu as une équation du second degré donc go la résoudre au lieu de faire un raisonnement qui ne ressemble strictement à rien.

• Méthode 1 : Solution évidente ?
• Méthode 2 : Si a est racine, avec nous pouvons factoriser par (x-a).
• Méthode 3 : Équation produit - si tu as alors P(X) = 0 ou Q(X) = 0
• Méthode 4 : Pensez aux identités remarques (a-b)^2, (a+b)^2, a^2 - b^2, ...
• Méthode 5 : Si les autres méthodes ne fonctionnent pas, on sort le Delta = b^2 - 4ac et on a en déduit les solutions.

[Helpme38]

Oula non, tu ne peux pas faire ça.
Il faut que utilise le discriminant et le calcul des racines pour résoudre cette équation.

b²-4ac
12²-4x3x9
144-108
= 36

x1= (-12 +sqrt{36} ) /2x3
= (-16 sqrt{3} sqrt{3}) /6

x2=(-12 -sqrt{36} ) /2x3
= (8 sqrt{3} sqrt{3}) /6

[Cheche]

go simplifier tes fractions plz

[mcar0nd]

b²-4ac
12²-4x3x9
144-108
= 36

x1= (-12 +sqrt{36} ) /2x3
= (-16 sqrt{3} sqrt{3}) /6

x2=(-12 -sqrt{36} ) /2x3
= (8 sqrt{3} sqrt{3}) /6

Euh oui, c'est ça, les solutions sont et mais tu peux encore les simplifier, beaucoup même.

[Helpme38]

Euh oui, c'est ça, les solutions sont et mais tu peux encore les simplifier, beaucoup même.

x1=\frac{-8+sqrt{3}sqrt{3}}{6}
x2=\frac{-16-sqrt{3}sqrt{3}}{6}

je peux encore plus là ??

[Cheche]

Tu nous expliques comment tu as fait ton calcul ???

Remarque très conne :

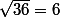
[Helpme38]

Tu nous expliques comment tu as fait ton calcul ???

Remarque très conne :

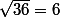
j'avait prit avec racine de quatre et trois :lol3:

[mcar0nd]

x1=\frac{-8+sqrt{3}sqrt{3}}{6}
x2=\frac{-16-sqrt{3}sqrt{3}}{6}

je peux encore plus là ??

Oula, je sais ce que tu as voulu faire ici.
Mais tout simplement, . Tu fais pareil pour la deuxième solution.

[Helpme38]

Oula, je sais ce que tu as voulu faire ici.
Mais tout simplement, . Tu fais pareil pour la deuxième solution.

d'accord sa j'ai compris, j'ai aussi fait mon tableau de variation calculer les minimums et maximums mais je ne voit pas ce que l'on me demande de faire dans les questions 4 et 5.

[Cheche]

Il faut étudier le signe, quand est-ce que c'est positif et quand est-ce que c'est négatif.
Revois la représentation graphique des fonctions de la forme : y = ax^2 + bx +c, ça te facilitera la tâche car tes remarques donnent l'impression que tu ne vois pas trop à quoi elle ressemble.

[Helpme38]

d'accord merci pour votre aide mcar0nd & Cheche!