Bonjour
voici l'exercice qui me pose problème (en particulier la question 5.)
Pouvez-vous m'aider ? Merci d'avance
Calcul de sommes
Soit S=1+2+3+...+2003+2004+2005
1. En remarquant qu'on a aussi:
S=2005+2004+2003+...+3+2+1,
calculer S+S et en déduire S.
Indication : 2005+1=2006
2004+2=2006
2. Généraliser en donnant la valeur de : 1+2+3+...+n
3. Soit P=2+4+6+8+...+2k, k étant un entier naturel non nul. Montrer que P =k (k+1)
4. Soit I=1+3+5+...+(2k+1). Calculer P+I et en déduire que I=(k+1)²
5. En déduire que : A = 1²-2²+3²-4²+...+2001² -2002²+2003²-2004²+2005²
Merci d'avance
Devoir maison calcul de sommes
4 messages
- Page 1 sur 1
le 5 n'est effectivement pas facile.
Tu as 2 solutions :
Soit dans A = 1²-2²+3²-4²+...+2001² -2002²+2003²-2004²+2005² tu factorise les nombres 2 à deux en utilisant a²-b²=(a-b)(a+b) , donc 1²-2²=-3 , 3²-4²=-7 , 5²-6²=-11
et il faut alors observer que la suite obtenue est une suite arithmétique de raison -4
Soit tu résous comme ça :
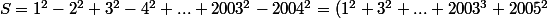 - (2^2 + 4^2 + ... + 2004^2 ))
^2 } } \right) - \left( \Big\sum\limits_{k = 1}^{1002} {(2k)^2 } \right) = 1 + \Big\sum\limits_{k = 1}^{1002} {\left( {(2k + 1)^2 - (2k)^2 } \right)})
} = 1 + \left( {4 \times \frac{{1002 \times 1003}}{2} + 1 \times 1002} \right) = 2011015)
Tu as 2 solutions :
Soit dans A = 1²-2²+3²-4²+...+2001² -2002²+2003²-2004²+2005² tu factorise les nombres 2 à deux en utilisant a²-b²=(a-b)(a+b) , donc 1²-2²=-3 , 3²-4²=-7 , 5²-6²=-11
et il faut alors observer que la suite obtenue est une suite arithmétique de raison -4
Soit tu résous comme ça :
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
