DEVOIR MAISON 1ere S

[MAMOUNE64]

Notre professeur de mathématique nous a donner un devoir maison en trois partie et j'ai un peu de mal à le faire, il faut utiliser le logiciel géogebra. :mur:
ABC est un triangle.
P est un point de (BC) distinct de B eet C tel que (vecteur)PB = a(vecteur) PC
Q est un point de (AC) distinct de A et C tel que (vecteur) QC =b (vecteur)QA
R est un point de (AB) distinct de A et B tel que (vecteur) RA = c(vecteur)RB

Partie A : élément de base

1) Justifier que les réels a,b,c ne sont ni nuls, ni égale a 1
2) Travail sur géogébra
Construire un triangle ABC ainsi que les droites (AB),(AC) et (BC) ( en renomera d,e,f ces droites)
PLacer les points P,Q,R respectivement sur les droites (BC),(AC) et (AB) distincts des sommets.
Faire afficher les réel a,b,c. Par exemple pour afficher a, saisir a=RapportColinéarite[P,C,B] en respectant bien l'ordre des points.
Faire afficher le produit p=abc

3) On se place dans le repère (A;(vecteur)AB;'vecteur)AC)
Decomposer les vecteurs AP,AQ et AR dans la base ( (vecteur)AB; (vecteur) AC )
Donner les coordonnées des points A,B,C,P,Q,R.
Ce que j'ai fait : J'ai reussi à faire la figure et à mettre les points j'ai un peu de mal à décomposer les vecteurs
Pour le vecteur AP jai mis AP= vecteur AB + Vecteur BP
= Vecteur AP- Vecteur PB
= vecteur AB- a vecteur PC
Pour les autres vecteur je n'ai pas réussi.
Je ne sais pas si ce que j'ai fait est juste.
Pour les coordonnées A(o;o) B(1;0) C(0;1) mais pour les autres points je n'ai aucune idée.

Parie B : théoreme de Ménélaüs

1- ( sur géogébra) Tracer la droite (PQ)
Quel lien peut-o, conjecture entre l'alignement des points P,Q et R et la valeur du produit abc ?
2 - Determiner les coordonées des vecteurs QR et QP
3 Démontrer que les points P,Q,R sont alignés si et seulement si, abc=1

Ce que j'ai fait 1) lorsque les points P,Q,R sont alignés ils se trouvent sur la droite (AB) le produit abc est donc nul
le reste je n'ai pas réussi.


Merci d'avance pour votre aide :help:

[Ben314]

Salut,
Concernant l'écriture (par exemple) du vecteur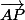 , la seule chose que tu sait concernant le point P, c'est que donc c'est évidement de là qu'il faut partir.
Tu veut obtenir un truc du style pour avoir les coordonnées de 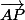dans la base .
Et, évidement LE outils, c'est la relation de Chasles.
Reste à voir comment "découper" les vecteurs dans pour n'avoir QUE des 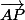, et (qu'il suffira de rassembler pour avoir la formule souhaitée)
Essaye...
(même méthode pour les autres vecteurs)

Ensuite, c'est avec ces résultat là que tu obtiendra les coordonnées de P,Q et R dans le repère (tes coordonnées pour A,B,C sont correctes)

De même, pour la partie 2, tu ne pourra faire des calculs qu'aprés avoir obtenu les coordonnées de P,Q,R dans la base (pour trouver des conditions pour qu'il soient alignés, c'est mieux d'avoir les coordonnées des points... :zen: )

[MAMOUNE64]

merci de votre réponse
vecteur AP= vecteur AB + vecteur BP c'est bien sa ?

[Ben314]

Je suis désolée mais j'ai un peu du mal à comprendre car on a aucune coordonnées et les exercices qu'on avait l'habitude faire il y'avait quelque indications et pas grand chose

Ca, ça veut dire que c'est les 'a', 'b' et 'c' qui te perturbent...
Si on prend par exemple a=3, c'est à dire , tu saurait me trouver les coordonnées de dans la base ?
Si oui, ben tu fait exactement totalement pareil avec 'a' à la place de 3.
Evidement le résultat dépend maintenant de a, mais la méthode est la même.

[MAMOUNE64]

Je ne pense pas que ce que j'ai écris soit juste mais je me lance
Vecteur AP=vecteur AB+vecteur BP
= vecteur AB - vecteur PB
= Vecteur AB - 3 Vecteur PC

[Ben314]

Moi, je ne partirais pas comme ça c'est à dire en commençant par écrire , bien que çe soit ça le résultat final qu'on veuille.

Je partirais plutôt de et j'écrirais que et que .
En procédant comme ça, j'ai immédiatement une égalité qui ne contient que les vecteurs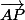 , et .
Aprés, je n'ai plus qu'à "ranger" les termes pour transformer cette égalité en un truc du style .

[MAMOUNE64]

Il faut donc faire cela : vecteur -AP+ Vecteur AB= - vecteur AP + vecteur AC ?

[Ben314]

Il faut donc faire cela : vecteur -AP+ Vecteur AB= 3 x ( - vecteur AP + vecteur AC ) ?

ne pas oublier le "3 fois" (voire même directement le "a fois")

[MAMOUNE64]

Alors - vecteur AP + vecteur AB = -a vecteur AC + a Vecteur AC
- vecteur AP+ A vecteur AP = vecteur Ab + a vecteur Ac

C'est bien sa ?

[Ben314]

Je te le fait avec 3 (tu le fera avec a et tu fera les autres).
On a :
et

donc l'égalité donnée par l'énoncé peut s'écrire sous la forme

En développant puis en ajoutant/retranchant des deux cotés, on en déduit que
c'est à dire que

[Ben314]

Alors - vecteur AP + vecteur AB = -a vecteur AP + a Vecteur AC
- vecteur AP+ a vecteur AP = - vecteur Ab + a vecteur Ac

C'est bien sa ?

oui (modulo une erreur de signe)

[MAMOUNE64]

- vecteur AP + vecteur AB= a(-vecteur AP + vecteur AC)
- vecteur AP + vecteur AB = -a vecteur AP + a vecteur AC
a vecteur AP - Vecteur AP = - Vecteur AB + a Vecteur AC
On a a AP -AP on obtient donc (a-1) ou pas

[Ben314]

obtient donc (a-1)

c'est ça.
Et tu as du expliquer dans la question 1) que 'a' était différent de 1 donc que l'on peut diviser par a-1 (qui est non nul).

[MAMOUNE64]

merci beaucoup AP est alors egale a = (a-1)/a AB + (a-1)/a AC ?

[MAMOUNE64]

juste une petite question pur AQ et AR il faut à chaque fois obtenir en reponse Ab et AC ou non

[Ben314]

juste une petite question pur AQ et AR il faut à chaque fois obtenir en reponse Ab et AC ou non

Oui, puisqu'on te demande les coordonnées des vecteurs dans la base (AB,AC)
Donc en fait, c'est un petit peu plus simple pour AQ et AR vu que dans la formule de départ (celle donnée par l'énoncé), il y a un des deux cotés ou il n'y a rien à faire : on a déjà (presque) AQ (ou AR)

[MAMOUNE64]

D'accord merci beaucoup pour votre aide
Les coordonnées de P c'est donc P(a-1/ ; a-1/a ) ?

[Ben314]

l'égalité donnée par l'énoncé peut s'écrire sous la forme

En développant puis en ajoutant/retranchant des deux cotés, on en déduit que
c'est à dire que


Donc les coordonnées de P dans le repère sont

[MAMOUNE64]

Pour AQ

On a QC=bQA
QC=QA+AC [CENTER] QA= QB + BA
= QB-AB
= b(QB-AB)
= bQB- bAB[/CENTER]

Je ne suis pas sur du tout pour QC

[Ben314]

QA= QB + BA

Ca, ç'est pas malin : tu veut tout exprimer à l'aide de AQ, AB et AC et là tu fait apparaitre du BQ alors que tu n'en veut pas...
Ce coup çi, il faut juste dire que QA=-AQ et c'est tout.