Devoir de cned
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
puppy92
- Membre Naturel
- Messages: 18
- Enregistré le: 12 Juil 2006, 17:08
-
 par puppy92 » 12 Juil 2006, 21:15
par puppy92 » 12 Juil 2006, 21:15
ben enfait je pense que c'est pas utile de le savoir parce je veux avoir cette expression simplifier mais enfait l'exo c'est:
f(x)= (x-1)/(x+3)
soit Un la suite définie par son premier terme U0=3 et par la relation de recurrence Un+1= f(Un)
a) faire apparaitre sur un graphique les termes U0 U1 U2 et U3
b) on pose Vn= 1/(1+Un) montrer que la suite Vn est une suite arithmétique puis exprimer Vn en fonction de n
donc pour prouver que c'était une suite arithmétique j'ai fait Vn+1 - Vn mais j'y arrive pas...
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 12 Juil 2006, 21:21
par nekros » 12 Juil 2006, 21:21
Ton raisonnement est juste.
T'es sûr de l'expression de f(x) ?
Thomas G :zen:
-
puppy92
- Membre Naturel
- Messages: 18
- Enregistré le: 12 Juil 2006, 17:08
-
 par puppy92 » 12 Juil 2006, 21:26
par puppy92 » 12 Juil 2006, 21:26
ouè je suis sure
mais comment je fais après avoir fait Vn+1 - Vn= 1/ [1+U(n+1)] - 1/(1+Un) :hein:
-
mln
- Membre Relatif
- Messages: 131
- Enregistré le: 20 Avr 2006, 13:05
-
 par mln » 12 Juil 2006, 21:32
par mln » 12 Juil 2006, 21:32
après tu remplaces un+1 par f(un) tu simplifies et tu dois trouver 1/2.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 12 Juil 2006, 21:41
par nekros » 12 Juil 2006, 21:41
Tu as
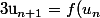=\frac{u_n+3}{2u_n+2})
Donc
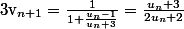
On a donc
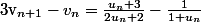
Donc
(1+u_n)-2u_n-2}{2(u_n+1)^2}=\frac{(u_n+1)^2}{2(u_n+1)^2})
Donc
)
est arithmétique de raison

Thomas G :zen:
-
puppy92
- Membre Naturel
- Messages: 18
- Enregistré le: 12 Juil 2006, 17:08
-
 par puppy92 » 12 Juil 2006, 21:52
par puppy92 » 12 Juil 2006, 21:52
ah ba oui je suis trop bête j'avais pas penser remplacer Un+1 par f(Un) merci beaucoup
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 12 Juil 2006, 22:03
par nekros » 12 Juil 2006, 22:03
Pour ma part de rien.
Et pour la dernière question, on sait que
)
est une suite arithmétique de raison

.
Par définition, on a donc
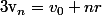
où

est la raison de la suite.
Donc

Thomas G :zen:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 12 Juil 2006, 22:09
par aviateurpilot » 12 Juil 2006, 22:09
dans ce cas

-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 12 Juil 2006, 22:18
par nekros » 12 Juil 2006, 22:18
Oui c'était le BUT de l'exercice.
Je trouve que c'est bien de chercher à quoi sert un exercice avant de l'entamer, pas toi ?
Thomas G :zen:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 12 Juil 2006, 22:37
par aviateurpilot » 12 Juil 2006, 22:37
oui :zen:
-
puppy92
- Membre Naturel
- Messages: 18
- Enregistré le: 12 Juil 2006, 17:08
-
 par puppy92 » 13 Juil 2006, 09:05
par puppy92 » 13 Juil 2006, 09:05
ah bon moi je croyais que Vn= V0 +nr = 1/4 + 1/2n= (2n+1)/4
-
puppy92
- Membre Naturel
- Messages: 18
- Enregistré le: 12 Juil 2006, 17:08
-
 par puppy92 » 13 Juil 2006, 09:07
par puppy92 » 13 Juil 2006, 09:07
En plus Un peut pas être égale à = (-n-4)/(6+n) parce que si on remplace n= 0 on trouve pas 3... alors qu'avec ce que j'ai fait on trouve Un = (-2n+3) / (2n+1)
-
mln
- Membre Relatif
- Messages: 131
- Enregistré le: 20 Avr 2006, 13:05
-
 par mln » 13 Juil 2006, 09:53
par mln » 13 Juil 2006, 09:53
je confirme : V0=1/4, ce qui donne
Vn=1/4+n/2
et Un=(-2n+3)/(2n+1)
-
puppy92
- Membre Naturel
- Messages: 18
- Enregistré le: 12 Juil 2006, 17:08
-
 par puppy92 » 13 Juil 2006, 14:37
par puppy92 » 13 Juil 2006, 14:37
j'ai une dernière question et après c'est fini :we:
soit la suite Un = [(n+1)/(3n)]^n
1) démontrer que 0< [(n+2)/(3n+3)]< (n+1)/(3n) <1
2) en déduire que la suite Un est décroissante
3) démontrer que 0< Un< (2/3)^n et déduisez en la limite de la suite Un
j'ai réussi la question 1) et 2) mais j'arrive pas la 3) :triste:
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 13 Juil 2006, 14:46
par Sdec25 » 13 Juil 2006, 14:46
Tu peux démontrer que
 ^n < \big(\frac 2 3 \big)^n)
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 13 Juil 2006, 15:59
par nekros » 13 Juil 2006, 15:59
Ne pas aller trop vite !!
Certes, on montre par récurrence le résultat suivant :
} < exp{nln{\frac{2}{3}})
Là on peut conclure que :
^n < (\frac{2}{3})^n})
Thomas G :zen:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 13 Juil 2006, 16:19
par nekros » 13 Juil 2006, 16:19
Ouais, tout ça revient au même...
Thomas G :zen:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 13 Juil 2006, 16:21
par aviateurpilot » 13 Juil 2006, 16:21
le plus court chemin
c'est mieux
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 13 Juil 2006, 16:26
par nekros » 13 Juil 2006, 16:26
Oui c'est vrai :ptdr:
Thomas G :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
