Devoir de cned
49 messages
- Page 1 sur 3 - 1, 2, 3
devoir de cned
bonjour à tous
alors j'ai un petit exercice du cned à faire et j'aurai besni d'aide
on considère les 2 suites (Un)et (vn) définies pour tout entier n>1 par:
un= 1^2+ 2^2+ 3^3+...+n^2 et vn=n(n+1)(2n+1)/6
1) calculer u1 u1 et u3 puis v1 v2 et v3
(j'ai trouvé u1=v1=1 u2=v2=5 et u3=v3=14)
2) exprimer un+1 - un puis vn+1 - vn en fonction de n
( j'ai trouvé (n+1)^2 pour les 2)
3) en déduire que pour tout entier n>1 un=vn
mais là je vois pas le rapport entre le fait que un+1 -un = vn+1 - vn et le fait que Un soit égale à Vn
merci d'avance
alors j'ai un petit exercice du cned à faire et j'aurai besni d'aide
on considère les 2 suites (Un)et (vn) définies pour tout entier n>1 par:
un= 1^2+ 2^2+ 3^3+...+n^2 et vn=n(n+1)(2n+1)/6
1) calculer u1 u1 et u3 puis v1 v2 et v3
(j'ai trouvé u1=v1=1 u2=v2=5 et u3=v3=14)
2) exprimer un+1 - un puis vn+1 - vn en fonction de n
( j'ai trouvé (n+1)^2 pour les 2)
3) en déduire que pour tout entier n>1 un=vn
mais là je vois pas le rapport entre le fait que un+1 -un = vn+1 - vn et le fait que Un soit égale à Vn
merci d'avance
Salut
tu peux regarder ce post
u1 = v1 et pour tout n, u(n+1) - u(n) = v(n+1)-v(n)
Donc on peut montrer que u(n) = v(n) pour tout n.
Si tu as u1 = v1, et que à chaque fois que n augmente on ajoute le même terme (n+1)^2, alors un = vn
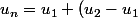 + ... + (u_n-u_{n-1}) = v_1 + (v_2 - v_1) + ... + (v_n - v_{n-1})) donc
donc 
tu peux regarder ce post
u1 = v1 et pour tout n, u(n+1) - u(n) = v(n+1)-v(n)
Donc on peut montrer que u(n) = v(n) pour tout n.
Si tu as u1 = v1, et que à chaque fois que n augmente on ajoute le même terme (n+1)^2, alors un = vn
merci beaucoup beaucoup
j'ai une autre question :we: j'espère que vous pourrez ncor m'aider
j'ai une suite Un = ((n+1)/3n)^n et je dois montrer si c'est une suite géométrique ou non donc j'essaie de calculer Un+1/Un pour voir si le quotient est constant ou non mais je suis bloquée à :
[(n+2)^(n+1) fois (3n)^n ] / [(3n+3)^(n+1) fois (n+1)^n] je sais pas trop comment faire pour simplifier ça ...
j'ai une autre question :we: j'espère que vous pourrez ncor m'aider
j'ai une suite Un = ((n+1)/3n)^n et je dois montrer si c'est une suite géométrique ou non donc j'essaie de calculer Un+1/Un pour voir si le quotient est constant ou non mais je suis bloquée à :
[(n+2)^(n+1) fois (3n)^n ] / [(3n+3)^(n+1) fois (n+1)^n] je sais pas trop comment faire pour simplifier ça ...
Pour la première question, je pense qu'il est plus simple de la traiter par récurrence :
Notons) la proposition "
la proposition " "
"
Initialisation :
Hérédité : supposons) vraie et montrons
vraie et montrons ) par récurrence pour tout
par récurrence pour tout 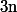 dans
dans 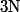 privé de 2
privé de 2
Soit dans
dans 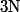 privé de 2
privé de 2
On a (d'après l'hypothèse)
(d'après l'hypothèse)
D'autre part, on a montré que
En additionnant les deux relations, on a
Donc) est vraie.
est vraie.
Conclusion, pour tout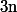 dans
dans 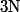 privé de 1, on a
privé de 1, on a 
Thomas G :zen:
Notons
Initialisation :
Hérédité : supposons
Soit
On a
D'autre part, on a montré que
En additionnant les deux relations, on a
Donc
Conclusion, pour tout
Thomas G :zen:
juste pour rire un peu :ptdr:
supposant que est geometrique
est geometrique
donc
donc^2=5(1+2+,,,+n^2))
donc^2=4(1+2+,,,+n^2))
donc (n+1)^2 est un multiple de 4 quelque soit n de IN*
donc n+1 est pair quel que soit n de IN*
donc n est impair quel que soit n de IN*
donc x=2 n'admet pas de solution dans IN*
ce qu'est absurde
alors n'ai pas geometrique :ptdr:
n'ai pas geometrique :ptdr:
supposant que
donc
donc
donc
donc (n+1)^2 est un multiple de 4 quelque soit n de IN*
donc n+1 est pair quel que soit n de IN*
donc n est impair quel que soit n de IN*
donc x=2 n'admet pas de solution dans IN*
ce qu'est absurde
alors
49 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
