Développer une expression
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
totor60
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Déc 2015, 19:50
-
 par totor60 » 31 Déc 2015, 12:56
par totor60 » 31 Déc 2015, 12:56
Bonjour à tous,
j'ai besoin d'aide, on me demande, dans un dm de maths de développer une expression : (x-1/2)².
Je la développe grace aux identités remarquables et je trouve x²-x+1/4. On me demande ensuite de déduire que x²-x-1 = (x-1/2)²-5/4 et la je ne sait plus comment faire !!!
Ai-je fait une erreur dans le premier calcul ou non ?
En espérant que vous pourrez m'aider !
Merci d'avance

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 31 Déc 2015, 13:14
par laetidom » 31 Déc 2015, 13:14
Bonjour,
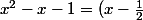^2 - (\frac{1}{2})^2 - 1)
et -
^2 - 1 = - \frac{5}{4}^)
-
totor60
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Déc 2015, 19:50
-
 par totor60 » 31 Déc 2015, 13:24
par totor60 » 31 Déc 2015, 13:24
donc dans cette expression , x² = (x-1/2)² ; x =(1/2)² c'est cela ?

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 31 Déc 2015, 13:29
par laetidom » 31 Déc 2015, 13:29
totor60 a écrit:donc dans cette expression , x² = (x-1/2)² ; x =(1/2)² c'est cela ?
j'ai pris d'abord les 2 premiers termes : x²-x et je me dis ça ressemble à a² - 2ab de a²-2ab +b² = (a-b)² donc
je fais comme si j'avais les 3 termes au début : x²-x= (x -1/2)² auquel je retranche le 3è terme -(1/2)²
donc j'obtiens (x -1/2)² - (1/2)² auquel je rajoute le -1 de la première expression, ça donne :
(x -1/2)² - (1/2)² - 1 = ...
-
totor60
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Déc 2015, 19:50
-
 par totor60 » 31 Déc 2015, 13:31
par totor60 » 31 Déc 2015, 13:31
On me demande ensuite de factoriser l'expression (x-1/2)²-5/4 et d'en déduire que les solutions dans IR de l'équation x²-x-1=0
La encore je ne comprend malheureusement pas !
Pouvez-vous m'aider sur ce point la ?
-
totor60
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Déc 2015, 19:50
-
 par totor60 » 31 Déc 2015, 13:32
par totor60 » 31 Déc 2015, 13:32
ok je comprend mieux ! merci
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 31 Déc 2015, 13:33
par Carpate » 31 Déc 2015, 13:33
totor60 a écrit:Bonjour à tous,
j'ai besoin d'aide, on me demande, dans un dm de maths de développer une expression : (x-1/2)².
Je la développe grace aux identités remarquables et je trouve x²-x+1/4. On me demande ensuite de déduire que x²-x-1 = (x-1/2)²-5/4 et la je ne sait plus comment faire !!!
Ai-je fait une erreur dans le premier calcul ou non ?
En espérant que vous pourrez m'aider !
Merci d'avance
Si
^2=x^2-x+\frac14)
Combien vaut
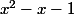
ou autrement dit que faut-il ajouter ou soustraire à
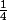
pour obtenir

?
Grave question !

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 31 Déc 2015, 13:33
par laetidom » 31 Déc 2015, 13:33
totor60 a écrit:On me demande ensuite de factoriser l'expression (x-1/2)²-5/4 et d'en déduire que les solutions dans IR de l'équation x²-x-1=0
La encore je ne comprend malheureusement pas !
Pouvez-vous m'aider sur ce point la ?
(x-1/2)² -5/4 = (x-1/2)² -
^2)
= " a² - b² "= ...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 31 Déc 2015, 13:47
par zygomatique » 31 Déc 2015, 13:47
laetidom a écrit:Bonjour,
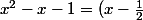^2 - (\frac{1}{2})^2 - 1)
et -
^2 - 1 = - \frac{5}{4}^)
salut
ce n'est pas vraiment ainsi qu'il faut répondre .... mais plutôt ::

...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
totor60
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Déc 2015, 19:50
-
 par totor60 » 31 Déc 2015, 14:57
par totor60 » 31 Déc 2015, 14:57
Carpate a écrit:Si
^2=x^2-x+\frac14)
Combien vaut
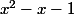
ou autrement dit que faut-il ajouter ou soustraire à
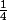
pour obtenir

?
Grave question !
x²-x-1 vaut (x-1/2)²-5/4
-
totor60
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Déc 2015, 19:50
-
 par totor60 » 31 Déc 2015, 15:06
par totor60 » 31 Déc 2015, 15:06
ensuite, comme je le disait tout àl'heure, il me faut factoriser (x-1/2)²-5/4 sur les conseils de laetidom, j'arrive au résultat suivant : (x-(1+racine5/2))(x-(1-racine5/2))
On me demande, pour conclure ce dm d'en déduire que les solutions dans IR de l'équation x²-x-1=0 qui comprend cette formulation et que faut-il y répondre ?

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 31 Déc 2015, 15:50
par laetidom » 31 Déc 2015, 15:50
zygomatique a écrit:salut
ce n'est pas vraiment ainsi qu'il faut répondre .... mais plutôt ::

...
salut,
effectivement :
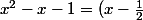^2 - (\frac{1}{2})^2 - 1 = (x-\frac{1}{2})^2 - \frac{1}{4} - \frac{4}{4} = (x-\frac{1}{2})^2 - \frac{5}{4})
pour répondre à la question qui m'était posée, de plus on peut rajouter que :

pour montrer le lien qu'il y a entre les 2 trinômes...

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 31 Déc 2015, 15:52
par laetidom » 31 Déc 2015, 15:52
totor60 a écrit:ensuite, comme je le disait tout àl'heure, il me faut factoriser (x-1/2)²-5/4 sur les conseils de laetidom, j'arrive au résultat suivant : (x-(1+racine5/2))(x-(1-racine5/2))
On me demande, pour conclure ce dm d'en déduire que les solutions dans IR de l'équation x²-x-1=0 qui comprend cette formulation et que faut-il y répondre ?
si
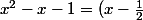^2 - \frac{5}{4} = (x-\frac{1}{2})^2 - (\frac{\sqrt{5}}{2})^2 = (x-\frac{1}{2} - \frac{\sqrt{5}}{2})(x-\frac{1}{2} + \frac{\sqrt{5}}{2}) = (x-\frac{1 + \sqrt{5}}{2})(x-\frac{1 - \sqrt{5}}{2}) = 0)
donc

ou
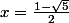
que tu peux visualiser sur le graphe :
http://www.cjoint.com/c/ELFpfQJpAYf
-
totor60
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Déc 2015, 19:50
-
 par totor60 » 31 Déc 2015, 16:00
par totor60 » 31 Déc 2015, 16:00
laetidom a écrit:je regardes...
super merci !
-
totor60
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Déc 2015, 19:50
-
 par totor60 » 31 Déc 2015, 16:06
par totor60 » 31 Déc 2015, 16:06
Donc l'équation n'admet qu'une solution : 0 c'est cela ?

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 31 Déc 2015, 16:07
par laetidom » 31 Déc 2015, 16:07
totor60 a écrit:Donc l'équation n'admet qu'une solution : 0 c'est cela ?
Non 2 !, regarde le graphe, la courbe coupe 2 fois l'axe des abscisses d'équation y=0,
ce qui est égal à 0 c'est l'équation, les 2 solutions sont - 0.618.... et +1.618....
-
totor60
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Déc 2015, 19:50
-
 par totor60 » 31 Déc 2015, 16:11
par totor60 » 31 Déc 2015, 16:11
laetidom a écrit:Non 2 !, regarde le graphe, la courbe coupe 2 fois l'axe des abscisses (y=0)
ce qui est égal à 0 c'est l'équation, les 2 solutions sont - 0.618.... et +1.618....
ah oui d'accord j'ai compris ! merci beaucoup de votre aide !

-
laetidom
- Habitué(e)
- Messages: 5720
- Enregistré le: 16 Déc 2013, 16:15
-
 par laetidom » 31 Déc 2015, 16:14
par laetidom » 31 Déc 2015, 16:14
totor60 a écrit:ah oui d'accord j'ai compris ! merci beaucoup de votre aide !
Ce fut un plaisir ! Bon réveillon !....Les deux solutions sont :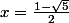
= - 0.618...

= 1.618...(c'est le nombre d'or !)
-
totor60
- Membre Naturel
- Messages: 20
- Enregistré le: 30 Déc 2015, 19:50
-
 par totor60 » 31 Déc 2015, 16:32
par totor60 » 31 Déc 2015, 16:32
laetidom a écrit:Ce fut un plaisir ! Bon réveillon !....Les deux solutions sont :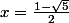
= - 0.618...

= 1.618...(c'est le nombre d'or !)
oui ! merci à vous aussi !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
