Bonjour.
"J-R" a écrit:1) qu'est ce que ca change si on fait un DL d'ordre 6 ou d'ordre 10 ?
Ça change la qualité de l'approximation de ta fonction au voisinage du point considéré : un DL10 est plus précis qu'un DL6, parce que la quantité négligée est plus petite. Accessoirement, pour peu que ta fonction soit un peu compliquée, ça peut radicalement changer le temps de calcul du DL...
"J-R" a écrit:2) pourquoi si on fait un DL d'ordre n on doit nécessairement obtenir un polynome de degré n quite à supprimer de plus haut degré ?
par exemple un DL en 0 d'ordre 3 de cos(x) c'est :
=1+\frac{h^2}{2} + h^3 \epsilon(h))
.
mais on l'aurais fait à l'ordre 1 il faudrait "supprimer" les h^2 et h^3 ?
(Attention, c'est
)
)
On n'obtient pas toujours un polynôme de degré n, mais un polynôme de degré inférieur ou égal à n. Ce qui est appelé l'ordre du DL, c'est l'ordre du reste, c'est-à-dire ton
)
, qu'on note en général
)
. Ici l'ordre du reste est 3, c'est-à-dire qu'on sait que le quotient de cette quantité par
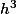
tend vers 0 en 0. Si on avait fait un DL1, le reste aurait été d'ordre 1, un
)
, et le terme

aurait été inclus dedans, puisqu'il est négligeable devant h en 0 (le quotient

tend bien vers 0 en 0).
D'une manière générale, si on connaît le DL à l'ordre n d'une fonction f en

, la partie polynômiale du DL à l'ordre
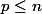
de f en

s'obtient en tronquant la partie polynômiale du DLn au degré p, ce qui est logique puisque les termes en
^k)
avec

sont négligeables devant
^p)
en

, on ne les supprime pas, ils sont inclus dans le reste d'ordre p.
"J-R" a écrit:commnet choisir l'ordre de notre Dl.
par exemple on nous donne une limite à calculer:
-x}{x^5})
là j'avais fait un DL d'ordre 6 de
)
et j'avais obtenu
)
? mais j'ai fait à l'ordre 6 comme j'aurais pu le faire à l'ordre 3 ?
Le choix de l'ordre du DL dans un calcul de limite demande un peu d'expérience, a priori y a pas de règle absolue, faut en quelque sorte anticiper ce que va donner ton DL, pour que tu puisses te retrouver avec un "terme significatif" qui te donnera la limite. Dans ton cas, le dénominateur est
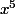
, donc un DL5 de
)
suffit, et on obtient
-x}{x^5}=-\frac12+\frac{1}{x^2}-\frac{1}{x^4}+o(1))
si mes calculs sont bons. Avec un DL3, on obtient
-x}{x^5}=\frac{1}{x^2}-\frac1{x^4}+\frac{o(x^3)}{x^5})
, et on ne peut pas conclure puisqu'on ne connaît pas la limite de
}{x^5})
.
En ce qui concerne la formule de Mac Laurin, qui je suppose est celle que je connais sous le nom de formule de Taylor avec reste Lagrange, je ne sais pas vraiment d'où elle vient, mais je suppose que les factorielles sont liées aux dérivées successives des polynômes, l'idée du DL étant l'approximation d'une fonction par un polynôme.
Voilà, en espérant t'avoir éclairé =)
