Déterminer la limite d'une suite géométrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par arthur terminal s » 18 Sep 2013, 19:09
par arthur terminal s » 18 Sep 2013, 19:09
bonjour à tous,
me voila devant un exercice fort dur à mon goût :
pour tout entier naturel non nul n, on pose Sn= "somme" Uk et Tn= >Sn/n²
1) exprimer Sn en fonction de n
2) déterminer la limite de la suite (Tn)
concernant la 1) ce me semble que Sn= (1-q^n)/(1-q) (formule suite géométrique)
concernant la 2) et bien....
merci d'avance de votre aide ! :zen:
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 18 Sep 2013, 19:35
par XENSECP » 18 Sep 2013, 19:35
Salut,
Tu peux donner la définition de (Un) stp?
 par arthur terminal s » 18 Sep 2013, 21:23
par arthur terminal s » 18 Sep 2013, 21:23
Bien sùr, bien que je ne vois pas le lien puisque Un n'est pas mentionné dans cette question.... c'est eux être la mon problème ^^ Un+1= 2/3 * Un + 1/3 * (n+1)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 18 Sep 2013, 21:29
par XENSECP » 18 Sep 2013, 21:29
Un est pas géométrique...
 par arthur terminal s » 18 Sep 2013, 21:32
par arthur terminal s » 18 Sep 2013, 21:32
Non mais en rapport avec la question une, "symbole somme" Uk est bien la somme dune suite géométrique nommée ici Sn
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 18 Sep 2013, 21:46
par XENSECP » 18 Sep 2013, 21:46
... Un n'est pas géométrique donc Sn peut pas être la somme d'une suite géométrique!!!

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 19 Sep 2013, 08:33
par chan79 » 19 Sep 2013, 08:33
arthur terminal s a écrit:Hum... des pistes alors ?
salut
tu peux d'abord exprimer

en fonction de n de la façon suivante:
tu passes par

tu cherches k et k' pour que

soit géométrique (de raison 2/3)
tu trouves k=-1 et k'=2
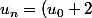 \times (\fra{2}{3})^n +n-2)
Tu en déduis

puis

qui tend vers
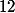
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
