Déterminer les réels a, b, c tels que...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
pra95
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Nov 2008, 19:06
-
 par pra95 » 27 Nov 2008, 19:16
par pra95 » 27 Nov 2008, 19:16
La fonction f est définie sur I=]-1;+

[ par f(x) =
(x^2+3x+3)}{(x+1)^2})
1) Déterminer les réels a, b, c tels que pour tout réel x de I, on ait : f(x) = ax +
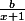
+
^2})
Merci d'avance pour vos réponses.
-
axiome
- Membre Rationnel
- Messages: 883
- Enregistré le: 04 Mai 2006, 21:37
-
 par axiome » 27 Nov 2008, 19:26
par axiome » 27 Nov 2008, 19:26
pra95 a écrit:La fonction f est définie sur I=]-1;+infinie[ par f(x) = (x-1)(x²+3x+3)/(x+1)²
1) Déterminer les réels a, b, c tels que pour tout réel x de I, on ait : f(x) = ax + \frac{b}{x+1} + \frac{c}{(x+1)²}
Merci d'avance pour vos réponse.
Bonjour,
Ben, une des méthodes est de calculer :
^2})
de façon à remettre sur même dénominateur.
Ensuite, tu calcules :
=\frac{(x-1)(x^2+3x+3)}{(x+1)^2})
: tu développes le numérateur.
Il ne te reste plus qu'à identifier les coefficients après...
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 27 Nov 2008, 19:28
par Timothé Lefebvre » 27 Nov 2008, 19:28
Bonsoir, merci de mettre ton message aux normes du forum le plus rapidement possible (cf. règlement ci-dessous).
-
pra95
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Nov 2008, 19:06
-
 par pra95 » 27 Nov 2008, 19:30
par pra95 » 27 Nov 2008, 19:30
Timothé Lefebvre a écrit:Bonsoir, merci de mettre ton message aux normes du forum le plus rapidement possible (cf. règlement ci-dessous).
C'est fait, je suis newbie DSL :we:
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 27 Nov 2008, 19:31
par Timothé Lefebvre » 27 Nov 2008, 19:31
pra95 a écrit:C'est fait, je suis newbie DSL :we:
Je faisais réference au début de ton message.
-
pra95
- Membre Naturel
- Messages: 27
- Enregistré le: 27 Nov 2008, 19:06
-
 par pra95 » 27 Nov 2008, 20:07
par pra95 » 27 Nov 2008, 20:07
axiome a écrit:Bonjour,
Ben, une des méthodes est de calculer :
^2})
de façon à remettre sur même dénominateur.
Ensuite, tu calcules
=\frac{(x-1)(x^2+3x+3)}{(x+1)^2})
: tu développes le numérateur.
Il ne te reste plus qu'à identifier les coefficients après...
Merci de ton aide, j'ai compris.
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 27 Nov 2008, 20:09
par Billball » 27 Nov 2008, 20:09
pra95 a écrit:Merci de ton aide, j'ai compris.
par contre prend soin de supprimer les 2 dénominateurs...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités