Determiner les reels a,b,c et asymptote (TES)urgent svp

[mmathstes1]

bonjour, j'ai un dm pour jeudi et je bloque pour cette question:

Soit la fonction définie sur ]-3;+oo[ par: f(x)=(x²-4)/(x+3)
On nomme T sa courbe réprésentative dans un repère orthogonal
2.a) Déterminer les réels a,b,et c tels que, pour tout x de l'intervalle]-3;+oo[:
f(x)= ax+b+(c/x+3).
J'attends vos réponses SVP

[Ericovitchi]

il te suffit de mettre ax+b+(c/x+3) au même dénominateur et d'identifier chaque terme avec ta fraction d'origine (car l'égalité étant vraie pour tout x, chaque terme doit être identique). Ça te fera un système en a,b,c.

[Olympus]

Salut !

Ou alors de diviser le polynôme x²-4 par x+3 .

[Ericovitchi]

oui mais souvent, ils n'ont pas encore appris la division euclidienne de 2 polynômes. Mais si tu connais, effectivement, c'est plus rapide.

Tu peux même aussi tant que l'on y est écrire x²-4 = (x-3)(x+3) + 5 et tu arrives directos au résultat

[mmathstes1]

il te suffit de mettre ax+b+(c/x+3) au même dénominateur et d'identifier chaque terme avec ta fraction d'origine (car l'égalité étant vraie pour tout x, chaque terme doit être identique). Ça te fera un système en a,b,c.

si j'ai bien compris en mettant chaque terme au mm denominateur cela donne:
(ax²+3ax+bx+c)/x+3
et apres je fait :ax²/x+3=x²-4
et ainsi de suite?

[Olympus]

oui mais souvent, ils n'ont pas encore appris la division euclidienne de 2 polynômes. Mais si tu connais, effectivement, c'est plus rapide.

Le posteur est en terminale, et si je ne me trompe pas, d'après le site bacamaths.net, la division polynomiale est faite en 1ère ^^

[mmathstes1]

Le posteur est en terminale, et si je ne me trompe pas, d'après le site bacamaths.net, la division polynomiale est faite en 1ère ^^

je ne comprends rien :mur:

[Olympus]

si j'ai bien compris en mettant chaque terme au mm denominateur cela donne:
(ax²+3ax+bx+c)/x+3

OK

et apres je fait :ax²/x+3=x²-4
et ainsi de suite?

Non . Tu auras plutôt .

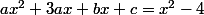
[mmathstes1]

OK


Non . Tu auras plutôt .

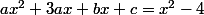
et apres ca fait :
a=1
3ax=0
bx=0
c=-4
?

[Olympus]

Non .

Plutôt : .

[mmathstes1]

Non .

Plutôt : .

ok merci
je trouve x-3 (-4/x+3)

[Ericovitchi]

et là tu vois que si tu avais écris x²-4 = (x-3)(x+3) + 5

alors était très rapide

(et montre aussi que tu as une faute quelque part. le terme constant ça n'était pas c mais 3b+c)

[mmathstes1]

et là tu vois que si tu avais écris x²-4 = (x-3)(x+3) + 5

alors était très rapide

(et montre aussi que tu as une faute quelque part. le terme constant ça n'était pas c mais 3b+c)

carrement plus simple! mais alors (x²-4)/(x+3) est different de ax+b+(c/x+3)
je ne comprends pas l'interet de la question

[Olympus]

(ax²+3ax+bx+c)/x+3

L'erreur vient du fait que je n'ai pas remarqué qu'il avait fait une faute après avoir mis au même dénominateur, c'est plutôt .

Mais la méthode restera la même .

[Ericovitchi]

pourquoi différent ? non c'est égal. (x²-4)/(x+2) = x-3 + 5 /(x+3)
je n'ai pas compris ce que tu voulais dire ?

L’intérêt de la question est que sous la forme x-3 + 5 /(x+3) on fait apparaître l'asymptote oblique de la fonction (y=x-3)


En tous les cas, corriges ton système d'équation
a=1
3a+b=0 donc b=-3
3b+c=-4 donc c=-4+9=5