peut tu juste m'aider sur la formulation du systheme ?
apres je le resoudrais merci
Determiner l'expression de f
44 messages
- Page 3 sur 3 - 1, 2, 3
Je vais essayer de te réexpliquer le principe
tu sais que ta fonction est un polynome de degré 3 et qu' il est impaire
alors, d' apres ton cours, ca veut dire que f(-x)=-f(x)
f(-x)=^3+b(-x)^2+c(-x)+d<br />f(-x)=-ax^3+bx^2-cx+d<br /><br />-f(x)=-ax^3-bx^2-cx-d)
comme ca doit etre egal, cela veut dire que les coeff de ces 2 polynomes doivent etre egaux 2 à 2
c' est à dire que
-a=-a (ici rien de particulier à dire c' est normal)
+b=-b donc b=0
-c=-c (rien de spécial à dire)
+d=-d donc d=0
donc en fait, les coeff b et d devant etre nuls, on a
=ax^3+cx)
il nous reste à trouver combien vaut a et combien vaut c
Pour cela tu utilises tes images c'est à dire:
f(3)=18 donc quand on remplace x par 3 ca doit valoir 18
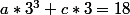
de meme avec f(-1)=2
^3+c*(-1)=2)
il te reste à resoudre ce systeme de 2 equations à 2 inconnus et tu trouveras a et c
ensuite tu réecris f(x) avec les valeur a et c que tu as trouvé
tu sais que ta fonction est un polynome de degré 3 et qu' il est impaire
alors, d' apres ton cours, ca veut dire que f(-x)=-f(x)
f(-x)=
comme ca doit etre egal, cela veut dire que les coeff de ces 2 polynomes doivent etre egaux 2 à 2
c' est à dire que
-a=-a (ici rien de particulier à dire c' est normal)
+b=-b donc b=0
-c=-c (rien de spécial à dire)
+d=-d donc d=0
donc en fait, les coeff b et d devant etre nuls, on a
il nous reste à trouver combien vaut a et combien vaut c
Pour cela tu utilises tes images c'est à dire:
f(3)=18 donc quand on remplace x par 3 ca doit valoir 18
de meme avec f(-1)=2
il te reste à resoudre ce systeme de 2 equations à 2 inconnus et tu trouveras a et c
ensuite tu réecris f(x) avec les valeur a et c que tu as trouvé
44 messages
- Page 3 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
