Détermination de Tangentes

[EnzOw]

Salut a Tous. Une fois de Plus j'ai un problème sur un Exo pour montrer les paraboles tangentes a une droite en un point donné :

Dans un repere choisi, on note d la droite d'equation y = x + 2 et A le point d'abscisse 0 de cette droite. ON se propose de determiner toutes les paraboles P d'equation y = ax² + bx + c, a different de 0 qui sont tangentes a d en A.

1) Démontrez que chacune de ces paraboles a une equation de la forme y = ax² + x + 2

2) x0 et y0 sont les coordonnées du sommet d'une parabole P
trouver une relation entre xo et y0 qui ne contient pas a

3) démontrez que les sommets des paraboles P sont sur une courbe fixe dont vous donnerez une équation

Je sais même pas par ou commencer :s
Merci de votre aide ++

[Elsa_toup]

Bonjour,

Je note f(x) = ax²+bx+c l'équation de la parabole P.
Si d est tangente à cette parabole en A, alors la pente de d est égale à celle de P en A.
La pente de d en A (comme partout) est 1.
Donc la pente de P (donnée par la dérivée de f en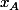 ) est 1.

De plus, f()=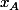

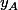
Je te laisse calculer, et en déduire f(x)

[EnzOw]

Ok merci je viens de comprendre ce qu'on recherchait :). Mais ca reste quand même flou pour la question 2.
La je ne vois vraiment pas comment le démontrer.
Le sommet d'une parabole est bien (-b/2a ; f(-b/2a))
x0 = -1/2a
y0 = f(-1/2a)

C'est deja un bon début ou je me plante complet ?

[Elsa_toup]

Non, ça a l'air bon...
En fait, je ne connais aps les formules, mais le sommet d'une parabole est le point en lequel la fonction atteint son minimum ou son maximum, soit le point en lequel la dérivée s'annule.

En passant par là, j'ai : 2ax+1 = 0, donc x=-1/(2a) et y=f(x)=f(-1/2a), donc tout comme toi.

Ceci dit, ça ne devrait pas contenir a ...
Je réfléchis ...

[EnzOw]

Dsl Mais j'ai encore un problème pour la question 1)
J'ai d : y = x+2
f(x) = x+2 donc f '(x) = 1 (coefficient directeur )
f(0) = 2 f' (0) = 1

P : g(x) = ax²+ bx +c donc g '(x) = 2ax + b
g(0) = c donc g' (0) = b
or g' (x) = f' (x) = 1 Donc b = 1 non ?

Mais comment je fais pour demontrer que y = ax² + x + 2
est ce que je peux dire f (0) = g (0) donc c = 2 ??

[Elsa_toup]

Oui, absolument. C'est ce que j'entendais par : f(xA)=yA

[EnzOw]

Ok pour le 2 j'ai xo = - 1 /2a et yo = f ( -1/2a )

a = -1/2xo

donc yo = f ( -1/xo ). Mais je ne sais pas si c'est ce que l'on recherche, si je dois allez plus loin ou pas ...

[Elsa_toup]

Non: .
Tu t'es emmêlé les pinceaux et tu tournes en rond là.
On a et = -1/2a
Le problème c'est qu'on ne répond pas à la question d'une manière ou d'une autre, puisqu'on nous demande de relier et sans faire intervenir a ...

[Starmac]

Bonjour,
Et pour la question 3 comment fait-on ?
Merci