Déterminants
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 23 Mar 2019, 06:25
par Dacu » 23 Mar 2019, 06:25
Bonjour à tous,
Soit

des fonctions polynomiales de degré pas plus que deux et
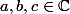
telles que
&Q(a)&R(a)\\P(b)&Q(b)&R(b)\\P(c)&Q(c)&R(c)\end{matrix}\right|=1)
.
Calculer la somme:
&Q(1)&R(1)\\P(b)&Q(b)&R(b)\\P(c)&Q(c)&R(c)\end{matrix}\right|+\left|\begin{matrix}P(a)&Q(a)&R(a)\\P(1)&Q(1)&R(1)\\P(c)&Q(c)&R(c)\end{matrix}\right|+\left|\begin{matrix}P(a)&Q(a)&R(a)\\P(b)&Q(b)&R(b)\\P(1)&Q(1)&R(1)\end{matrix}\right|)
.
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
aviateur
 par aviateur » 23 Mar 2019, 10:54
par aviateur » 23 Mar 2019, 10:54
Bonjour
Posons
=\left|<br />\begin{array}{ccc}<br /> P(a) & Q(a) & R(a) \\ P(b) & Q(b) & R(b) \\ P(c) & Q(c) & R(c)<br />\end{array}<br />\right|)
En utilisant le fait que P,Q et R sont degré 2 au plus, il est facile de voir que

est un polynôme homogène de degré 3, plus précisément
=K (a-b)(b-c)(c-a))
où K est une constante qu'il n'est pas utile de déterminer.
Alors soit

quelconque.
On a
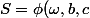+\phi(a,\omega,c)+\phi(a,b,\omega))
On remplace et on simplifie facilement d'où
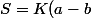(b-c)(c-a) =\phi(a,b,c))
Ce qui répond à l'exercice et le généralise.
C.Q.F.D
-
aviateur
 par aviateur » 24 Mar 2019, 06:59
par aviateur » 24 Mar 2019, 06:59
Bonjour
Visiblement tu n'as pas compris
Non seulement je réponds à
. ta question et je généralise
S dépend des 3 polynômes.
Si l'énoncé dit que S vaut 1 alors tu as la valeur
de K.
Mais le résultat est plus général
Cela ne dépend pas de S égal 1,
Et le nombre que j appelle oméga il peut être quelconque pas forcément 1 ni égal à S
1Bon maintenant on est sur un forum de maths
Il vaut lieux se fier à une bonne démonstration qu'aux dire
de '' certains'',
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 24 Mar 2019, 07:00
par Dacu » 24 Mar 2019, 07:00
aviateur a écrit:Bonjour
Posons
=\left|<br />\begin{array}{ccc}<br /> P(a) & Q(a) & R(a) \\ P(b) & Q(b) & R(b) \\ P(c) & Q(c) & R(c)<br />\end{array}<br />\right|)
En utilisant le fait que P,Q et R sont degré 2 au plus, il est facile de voir que

est un polynôme homogène de degré 3, plus précisément
=K (a-b)(b-c)(c-a))
où K est une constante qu'il n'est pas utile de déterminer.
Alors soit

quelconque.
On a
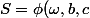+\phi(a,\omega,c)+\phi(a,b,\omega))
On remplace et on simplifie facilement d'où
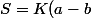(b-c)(c-a) =\phi(a,b,c))
Ce qui répond à l'exercice et le généralise.
C.Q.F.D
Bon matin,
Certains disent que

pour
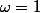
et vous dites que peu importe la valeur de

nous obtenons que

.Quelle est la valeur de

et comment calculons cette constante?Peut-être
(b-c)(c-a)})
?
Merci très beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
-
aviateur
 par aviateur » 24 Mar 2019, 07:00
par aviateur » 24 Mar 2019, 07:00
Bon j'ai pas vu ce que tu as ajouté
Et bien le vous dites''' ''
Et bien je n'ai pas dit cela
-
Dacu
- Membre Rationnel
- Messages: 627
- Enregistré le: 10 Mar 2013, 17:37
-
 par Dacu » 24 Mar 2019, 07:33
par Dacu » 24 Mar 2019, 07:33
aviateur a écrit:Bon j'ai pas vu ce que tu as ajouté
Et bien le vous dites''' ''
Et bien je n'ai pas dit cela
Si par hypothèse
=\left|<br />\begin{array}{ccc}<br /> P(a) & Q(a) & R(a) \\ P(b) & Q(b) & R(b) \\ P(c) & Q(c) & R(c)<br />\end{array}<br />\right| =1)
et
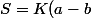(b-c)(c-a) =\phi(a,b,c)=1)
, alors il s'ensuit que
(b-c)(c-a)})
.Si
(b-c)(c-a)})
, alors comment calculer la valeur de

?
Merci très beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités

où K est une constante qu'il n'est pas utile de déterminer.
quelconque.