Descente infinie démo

[J-R]

bonsoir,

Soit suite infinie d'entiers naturels, décroissante au sens large.

Montrer que,à partir d'un certain rang, cette suite est stationnaire.

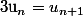
en fait il faut montrer que à partir d'un certain rang d'un rang p tel que ....

mais là je ne vois absolument pas comment faire.

d'après l'enoncé on peut écrire que et pis c'est tout....

merci

[emdro]

Décidément, JR, j'aime bien tes questions...

Par l'absurde, en supposant que ta suite à valeurs dans IN, décroissante, n'est pas stationnaire à partir d'un certain rang, qu'est-ce que cela signifie?

[J-R]

j'aimerais ce type de question quand je saurais les faire d'un clic.... :zen:

sinon elle n'est pas stationnaire si pour tout rang p tel que :,

le différent ne convient pas car j'ai juste pris la négation ....

[J-R]

ah non j'ai pas traduit le fait de la décroissance.... je cherche

[emdro]

Non, ou en tout cas, pas clair...

elle est stationnaire s'il existe p tel que pour tout n supérieur à p, Un=Up

Donc elle n'est pas stationnaire si:
pour tout p, il existe n supérieur à p, tel que Un différent de Up

Et en l'occurence, Un
OK?

[lapras]

salut,
Un est minorée par 0, tu es d'accord ?
car Un >= 0 pour tout n
Un est décroissante
Supposons que Un soit non stationnaire pour tout n>p
alors
pour n>p ,
Un < A
donc
Un appartient à ]-OO ; A]
donc Un devient négatif à partir d'un certain rang, ce qui est impossible : contradiction => Un stationnaire à partir d'un certain rang

[J-R]

oui d'accord je comprend mieux

ca c'est une contradiction de la strict décroissance ?

[J-R]

salut lapras ,

ah ba oui en fait c'est tout bete ne peut pas etre négatif ....

[lapras]

je ne suis pas sur de ma réponse j-R, emdro, peux tu confirmer ?

[emdro]

Supposons que Un soit non stationnaire pour tout n>p

C'est pas très clair.

alors
pour n>p ,
Un Un stationnaire à partir d'un certain rang

Je ne vois pas le moment précis où tu utilises le fait que la suite est à valeurs dans IN.

[J-R]

emdro avais une autre méthode puisqu'il m'indique le fait que ...

[lapras]

Emdro,
puisque Un est une suite infini d'entiers naturels, alors Un est >= 0 , nan ?
C'est de la que je dis que Un ne peut etre négatif
A c'est un entier naturel

[emdro]

Reprenons
(Un) n'est pas stationnaire donc:
pour tout p, il existe n supérieur à p, tel que Un différent de Up, et comme elle est décroissante, on aura Un
En vertu de cette idée, on peut trouver un rang n0 tel que Un0On peut trouver un rang N1 tel que Un1...

après U0 pas au maximum, on oblige la suite à devenir négative puisqu'elle descend de 1 au minimum à chaque fois.
c'est absurde.

NB Lapras avait toutes les bonnes idées. C'était simplement un peu mal rédigé...
Edit: j'ai remis les inégalités dans le bon sens. Désolé!

[emdro]

Emdro,
puisque Un est une suite infini d'entiers naturels, alors Un est >= 0 , nan ?
C'est de la que je dis que Un ne peut etre négatif

d'accord

A c'est un entier naturel

OK, mais c'est un nombre particulier (U0? U1?), c'est pour tout A, c'est Il existe un A?...

[lapras]

A = U0 si je ne me trompe pas

[J-R]

d'accord c'est compris :)

merci

a+

[emdro]

Un < A
donc
Un appartient à ]-OO ; A]
donc Un devient négatif à partir d'un certain rang, ce qui est impossible :

Si A est fixé comme tu le proposes (A=U0), dans ce cas Un appartient à ]-OO ; A] n'implique pas que Un devienne négatif à partir d'un certain rang. Il est juste entre 0 et A...

[emdro]

d'accord c'est à peu près compris

Il faut que cela le soit tout à fait!

Range ton ordinateur, et refais la démonstration dans ta tête...

[J-R]

si c'est bon j'ai modifié : justement je ne comprenais pas pourquoi Un0>U0 (j'avais fait mon dessin et je ne voyais pas jusqu'à ta modif)

mais là tout est clair :zen:

merci une fois de plus emdro :)

EDIT: j'ai oublier de préciser: en déduire : "Toute suite décroissante d'entiers naturels est finie" (si je n'abuse pas ce "principe" est de Fermat ?)

comme on a prouvé que (un) est stationnaire la suite est finie !! ya plus rien à démontrer ?

[emdro]

MY pleasure!