[Recherche] Des problèmes niveaux TS ?

[benekire2]

Bonsoir,

Certains s'en souviennent peut être, j'avais déjà demandé sur le forum des exos d'un niveau 1S qui puissent tenir 4 heures ...
Alors bien sûr je n'avais pas trouver !! Tous les problèmes niveau 1S qu'on m'avait proposé tenaient 1h voire 1h30 au max.

Aujourd'hui, je voudrais savoir si vous auriez des idées / et ou des problèmes déjà faits ( ça m'étonnerait franchement) qui puissent tenir un élève de TS ( en france) pendant 3 à 5 heures ?

En fait, je cherche a reconstituer des problèmes style concours mais avec un niveau de connaissances TS. J'aimerais que, comme les concours, le sujet soit centré sur un seul thème ...
Toutefois j'aimerais que le niveau ressemble à celui d'un concours ( bon ok c'est superflu vu tout ce que je demande !!)

Je vous remercie !!


PS: J'avais déjà des petits trucs genre racine de l'unité dans C , etude d'une inversion, suite de Fibonacci ( mais c'est pas génial ) ou fonction définie par uneintégrale, mais ça ne tient pas plus de 1h30 ...

[Anonyme]

Tu as le livre du génialissime Mr Alarcon,de LLG

[benekire2]

Je ne l'ai pas ... et vu qu'il est à LLG, je suis sur que les problèmes sont géniaux, mais je ne suis pas sur que ce soit trop niveau TS, je crois que ça mord vachement !!

Enfait ce n'est pas pour moi, mais pour donner à des TS ..

[Anonyme]

Si ça t'intéresse quand même, envoie moi un MP, j'ai le livre donc je peux te passer un ou deux problèmes intéressants.

[Nightmare]

Ca me parait dur de faire un problème de 5h d'un seul tenant vu le "peu" de bagage qu'on a au lycée. La seule chose que tu pourrais faire est d'introduire dans ton exercices de nouveau théorèmes que tu fais alors démontrer à l'élève.

[benekire2]

Tu me conseille quels théorèmes ? Sur les suites ? Intégration ? Après si on trouve deux trois résultats , on pourra "construire" un objectif du problème ...

[Olympus]

Prouve le théorème de Napoléon en utilisant uniquement les rotations :D ( on l'a déjà fait en classe nous, sauf que c'était sans les complexes ) .

[benekire2]

Prouve le théorème de Napoléon en utilisant uniquement les rotations ( on l'a déjà fait en classe nous, sauf que c'était sans les complexes ) .

Déjà fait ^^

[Olympus]

Grrr... Oki .

Etudes de fonctions :

Montrer que .

Résoudre dans l'équation suivante : .

[benekire2]

Grrr... Oki .

Etudes de fonctions :

Montrer que .

Résoudre dans l'équation suivante : .

La première je conaissais pas, mais la deuxième c'est fait ^^

Mais on ne peut pas tenir 4 heures sur ce genre d'exos ( j'entend par là qu'on doit mettre des questions intermédiaires, on ne va pas poser une OIM ... )

[Billball]

simplifier les expressions puis

si ca peut t'occuper ...!

[Olympus]

Des questions intermédiaires ... je pense que ceci t'intéresserait : http://perso.orange.fr/freddmn/annales/similitudes.pdf .

[poiuytreza]

Si tu veux des exos d'un bon niveau de Terminale sur lesquels tu peux tenir plusieurs heures, pourquoi tu cherches pas tout simplement des exos de CG ?

Sinon, même si c'est pas le même genre, tu as tous les exos de type IMO, qui sont (enfin, je trouve) bien plus jolis, mais ça a pas l'air d'être ce que tu cherches.

[benekire2]

@Billball
Oui mais on tient pas 4h avec des questions intermédiaires la dessus ...

[benekire2]

Des questions intermédiaires ... je pense que ceci t'intéresserait : http://perso.orange.fr/freddmn/annales/similitudes.pdf .

Ca sort pas du bacamath ?

Il me semble avoir rencontré pas mal de ces exos de bacs ..

[Zweig]

J'ai quelques problèmes qui vont te faire tenir au moins5h ... si ce n'est une journée entière (j'exagère ... ou pas :we:)

Par exemple, celui-ci, largement niveau T°S (au niveau des connaissances) :

Montrer que si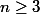 , alors il existe des naturels tels que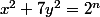

Pour la petite histoire, ce problème a été inventé par Euler qui ne l'a jamais publié. C'est que très récemment que des mathématiciens l'ont trouvé dans ses notes. Il a été proposé aux olympiades d'un pays de l'Est en 1985 : personne ne réussit à le résoudre. Il a été ensuite proposé à des arithméticiens de renommée internationale lors d'un test de 6h : personne ne le réussit.

Ou encore, très difficile :

Dans une compétition mathématique certains participants sont des amis.
L’amitié est toujours réciproque. Un groupe de participants est appel´e une clique si toute paire d’entre eux est formée de deux amis. (En particulier, chaque groupe d’au plus un participant constitue une clique.) Le nombre de participants dans une clique est appelé sa taille.

On suppose que, dans cette compétition, la plus grande taille des cliques est paire.

Montrer que les participants peuvent être répartis dans deux pièces de telle sorte que la plus grande taille des cliques contenues dans une de ces pièces soit égale à la plus grande taille des cliques contenues dans l’autre.

[Dinozzo13]

Salut !

Certains s'en souviennent peut être, j'avais déjà demandé sur le forum des exos d'un niveau 1S qui puissent tenir 4 heures.

Et comment :king2:
A croire que ce genre de problème si fastidieusement long n'existe pas pour le lycée malheureusement :cut: .
J'aimerai ajouter que la question m'intéresse égelement :++:

[Dinozzo13]

Par exemple, celui-ci, largement niveau T°S :

Montrer que si , alors il existe des naturels tels que

J'adore tes problème Zweig :++:
T'es un roi de l'arithmétique toi :ptdr:

[Zweig]

La solution est à se TIRER UNE BALLE dans la tête, je vous assure ... Elle est d'une simplicité biblique ... Alors que le problème est très difficile ...

Bref, l'Arithmétique dans toute sa splendeur !

[Dinozzo13]

C'est bien pour ça que j'adore l'arithmétique.