[Recherche] Des problèmes niveaux TS ?

par **benekire2** » 13 Mar 2010, 21:04

Zweig a écrit:La solution est à se TIRER UNE BALLE dans la tête, je vous assure ... Elle est d'une simplicité biblique ... Alors que le problème est très difficile ...

Bref, l'Arithmétique dans toute sa splendeur !

Je connais ce problème.

Cependant ce n'est vraiment pas le genre de problèmes que je cherche ... je cherche des choses style concours et pas olympiades .. La ce serait 5 heures de réfleions sur une question. Et on ne trouvera pas au bout de 5h.

Le problème a été posé aux IMO de l'année d'après, et selon moi si 11 ou 12 élèves ont trouvés la réponses c'est qu'ils s'étaient renseigné sur le problème posé aux olympiades d'un pays de l'est ( russie je crois .... ) et qu'ils ont obtenus la solution ...

La dose d'astuce a avoir la dessus est plus qu'olympique !!

par **Zweig** » 13 Mar 2010, 21:20

Au contraire, je ne trouve pas l'exercice astucieux ... Je trouve que la démarche au départ à effectuer est assez naturelle (le tableau), après ce qui fait la différence c'est la capacité à voir les choses ... Ce que je veux dire, c'est que le type qui a trouvé cette solution (un olympiadeur de l'équipe allemande) n'a pas utilisé un truc sorti de son chapeau ...

par **Zweig** » 13 Mar 2010, 21:21

Si tu veux des problèmes qiui te tiendront en haleine quelques temps, voir ici :

http://www.eleves.ens.fr/home/kortchem/cg.html

par **Doraki** » 13 Mar 2010, 21:28

Zweig a écrit:Par exemple, celui-ci, largement niveau T°S (au niveau des connaissances) :

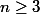
Montrer que si , alors il existe des naturels tels que

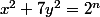
Pour la petite histoire, ce problème a été inventé par Euler qui ne l'a jamais publié. C'est que très récemment que des mathématiciens l'ont trouvé dans ses notes. Il a été proposé aux olympiades d'un pays de l'Est en 1985 : personne ne réussit à le résoudre. Il a été ensuite proposé à des arithméticiens de renommée internationale lors d'un test de 6h : personne ne le réussit.

Etant donné la simplicité du truc, j'ai peine à croire ce que tu rapportes o_O.
Ptetre que si on pas que la preuve tient en 3 lignes, c'est dur :/

par **Zweig** » 13 Mar 2010, 21:31

Ce que je rapporte est tiré du livre d'Arthur Engel "Problem Solving Strategies", je n'ai bien sûr pas pu le vérifier par moi-même ...

par **poiuytreza** » 13 Mar 2010, 21:32

Petite précision : x et y doivent être impairs (parce que c'est vrai que sinon il y a pas grand chose à faire :we: )
Si tu veux chercher des exos sympas de type IMO, tu n'est pas obligé de commencer par ceux qui sont considérés comme les plus durs de tous les temps...

Sinon dans le "style concours" tu as le concours général : c'est en rapport avec le programme, plus accessible que les IMO et il y a de quoi tenir 5 heures.

par **gigamesh** » 13 Mar 2010, 22:05

C'est du niveau 4e ton truc de x²+7y² =2^n....
Bon évidemment il faut savoir que 7+1=8 et 7+9=16...

par **Dinozzo13** » 14 Mar 2010, 02:39

:ptrdr : ben moi perso, à par un raisonnement par récurrence, je ne vois rien :triste: .

par **simson 57640** » 14 Mar 2010, 07:31

Soit Un Parrallogramma Abcd
E Milei De Bc
F Milieu De Dc

Il Fallait Demontrer Que Ac + Bd = 2bc
Facile Mais Je Bloque Pour Demontrer Que
Ae+af+3\2ac

Merci De Repondrre

par **benekire2** » 14 Mar 2010, 08:32

simson 57640 a écrit:Soit Un Parrallogramma Abcd
E Milei De Bc
F Milieu De Dc

Il Fallait Demontrer Que Ac + Bd = 2bc
Facile Mais Je Bloque Pour Demontrer Que
Ae+af+3\2ac

Merci De Repondrre

Sérieusement c'est vraiment l'endroit ? Ou alors tu comptait vraiment faire tennir un TS pendant 4 h ? :zen:

Pour te répondre, j'imagine que c'est envecteurs. Tes points E et F sont inutiles pour ta question, AC+BD=AB+BC+BC+CD=2BC

par **gigamesh** » 14 Mar 2010, 09:44

Pour Dinozzo : fais un dessin !
(Un carré c'est un quadrilatère avec 4 côtés égaux, et quatre angles droits)

Tu as un carré de x et sept carrés de y, et tu veux construire un carré de 2p si n=2p (prends x=3y) et un rectangle 2^p fois 2^(p+1) si n=2p+1 (prends x=y).

par **Zweig** » 14 Mar 2010, 09:55

gigamesh a écrit:C'est du niveau 4e ton truc de x²+7y² =2^n....
Bon évidemment il faut savoir que 7+1=8 et 7+9=16...

WTF ? Il faut montrer que POUR TOUT n, il existe de tels entiers x et y, là tu l'as juste montrer pour deux cas particuliers.

par **benekire2** » 14 Mar 2010, 10:05

Concours général il y en a des pas mal, c'est plus dans le style que je recherche :)

Par contre tout ce qui est IMO, c'est pas ça que je cherche.

Et ce n'est pas pour moi, donc je dois rendre le truc compréhensible :id:

par **poiuytreza** » 14 Mar 2010, 13:19

Zweig : le problème est que tu as oublié de préciser que x et y devaient être impairs. Sans cette condition, il suffit d'avoir des soplutions pour 8 et 16 et de les multiplier plusieurs fois par 2...

[Recherche] Des problèmes niveaux TS ?

Qui est en ligne