[Encore besoin d'aide] Des complexes??

par **Benk** » 06 Nov 2008, 20:16

Bonjour à tous, alors voila, il faut dire pour chaque affirmation si elle est vraie ou fausse en démontrant...Et dès le début, je bloque...Help please...

par **djanos** » 06 Nov 2008, 20:17

je pense que tu devrait essayer en posant z=x+iy

par **Benk** » 07 Nov 2008, 17:31

up please... J'arrive toutjours pas...

par **Sa Majesté** » 07 Nov 2008, 17:56

Bonjour,
Tu peux poser z=e^(it) et z'=e^(it')

par **Benk** » 07 Nov 2008, 18:54

Sa Majesté a écrit:Bonjour,
Tu peux poser z=e^(it) et z'=e^(it')

Eh bien en faisait ceci, j'arrive au résultat suivant:

Mais je n'aboutis pasencore à une expression sans les "i"...comment faire??

par **Sa Majesté** » 07 Nov 2008, 18:59

Tu aurais pu rester en e^(it) et e^(it')
Ensuite tu mets e^(i(t+t')/2) en facteur au numérateur et au dénominateur

par **Benk** » 07 Nov 2008, 19:13

Sa Majesté a écrit:Tu aurais pu rester en e^(it) et e^(it')
Ensuite tu mets e^(i(t+t')/2) en facteur au numérateur et au dénominateur

Mettons que je fasse comme tu le dis, voici ce que j'ai...

Alors là, je ne sais pas avancer..ou plutot, je ne peux plus avancer..si??

par **Sa Majesté** » 07 Nov 2008, 19:16

Si tu peux avancer
Mets e^(i(t+t')/2) en facteur au numérateur et au dénominateur

par **Benk** » 07 Nov 2008, 19:54

Merci de ton aide pour le a), maintenant, je dois dire que je bloque sur le b)...
J'ai essayé de remettre un terme en facteur, mais j'ai du mal, tout comme l'implication dans l'autre sens :mur: ... help please..

par **Sa Majesté** » 07 Nov 2008, 20:00

Qu'as-tu trouvé pour le a) ?
Pour le b), pose u=e^(it)

par **Benk** » 07 Nov 2008, 20:25

Sa Majesté a écrit:Qu'as-tu trouvé pour le a) ?
Pour le b), pose u=e^(it)

Eh bien j'aboutis à

Donc, on peut dire que Z est réel... C'est ça non??

Bon, et apres pour le b) et c), j'ai déja fais ce que tu m'as dit:

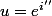
avec aussi

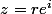
et "conjugué de z"=

mais j'arrive à ceci:

Je suis encore une fois bloqué...

par **Sa Majesté** » 07 Nov 2008, 20:32

Benk a écrit:Eh bien j'aboutis à

Donc, on peut dire que Z est réel... C'est ça non??

Oui :++:

Benk a écrit:Bon, et apres pour le b) et c), j'ai déja fais ce que tu m'as dit:

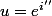
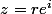
avec aussi et "conjugué de z"=

mais j'arrive à ceci:

Je suis encore une fois bloqué...

Tu pouvais laisser z sans le mettre sous forme exponentielle
Sinon tu mets e^(iT"/2) en facteur au numérateur et au dénominateur

par **Benk** » 07 Nov 2008, 21:25

J'arrive le b)... En effet j'arrive à :

Donc U est réel...mais comment faire la réciproque???

et pour le d) qui revint un peu sur le meme principe, comment dois-je faire?

par **Sa Majesté** » 07 Nov 2008, 21:32

Le c)
U est réel ssi U = Ubarre ... et ça vient tout seul :id:

par **Sa Majesté** » 07 Nov 2008, 21:38

Le d) est encore plus simple
Tu multiplies en haut et en bas par 1+iu et tu obtiens directement la partie réelle et la partie imaginaire, tu n'as plus qu'à calculer le module

[Encore besoin d'aide] Des complexes??

[Encore besoin d'aide] Des complexes??

Qui est en ligne