Des amateurs de suites géométriques?

[pierre71]

Voila l'eposé de mon problème. Je travaille sur une variable aléatoire discrète Y. Je dois calculer E(X) qui correspond à l'espérance mathématique de la variable.

Je trouve :


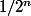
Soit la raison de la suite géométrique
Et le premier terme de la suite géométrique

Dans la correction de mon livre, il est marqué que ça c'est égal à 2. La je comprends pas comment on fait (c'est la somme de suites géométriques?).

Merci bien pour votre aide.

:++:

[becirj]

Bonjour
Je ne comprends pas trop la question. N'a-t-on pas plutôt une suite géométrique de raison , comprenant n termes et faut-il calculer une limite ? Quel est le premier terme de la suite ?

[pierre71]

on a :


E(X)=

Soit

Et dans le corrigé du livre

Alors moi, je comprends pas comment c'est égal à 2. J'ai supposé que l'on pouvait passer par les suites, mais je suis pas sûr?!

merci beaucoup

:marteau:

[pierre71]

on a :




Soit

Et dans le corrigé du livre

Alors moi, je comprends pas comment c'est égal à 2. J'ai supposé que l'on pouvait passer par les suites, mais je suis pas sûr?!

merci beaucoup

:marteau:

[becirj]

Ce n'est pas une suite géométrique. Il existe une méthode pour calculer cette somme mais elle est compliquée et on ne la devine pas si on ne l'a jamais vue de plus ce n'est que la limite de cette somme, quand n tend vers l'infini, qui est égale à 2.
Il faudrait voir exactement ce que dit ton livre.

[pierre71]

ok g compris, tu as raison, ce doit être la limite quand n tend vers + l'infini