Dérivées et tangentes !

[Jeandu57]

Et ben c'est bon ! Il existe donc deux solutions a telles que la courbe admette des tangentes en ces points d'abscisse a et passant par le point de coordonnées (0;1).
Détermine l'expression des deux tangentes, vérifie quelles sont conformes avec ta calculatrice et va te coucher

Au fait, je me suis trompée (encore :/) : il s'agit de T(x) et non pas de T(a) !

Julie

Pour déterminer les deux équations de tangentes, il faut remplacer mes deux solutions dans l'expression y =f'(a) ( x-a ) + f(a)
c'est ca ?

[globule rouge]

Pour déterminer les deux équations de tangentes, il faut remplacer mes deux solutions dans l'expression y =f'(a) ( x-a ) + f(a)
c'est ca ?

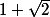
C'est exactement ça : tu remplaçeras successivement a par et par !

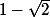
[Jeandu57]

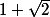
C'est exactement ça : tu remplaçeras successivement a par et par !

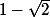
Ok, donc si je remplace par 1+ racine (2)

Je trouve 2x/(2+rac(2) )² + (8+4rac(2) ) / ( 2+rac(2) )²

C'est correct ?

[Jeandu57]

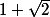
C'est exactement ça : tu remplaçeras successivement a par et par !

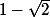
Et pour 1-rac(2) je trouve 2x / ( 2-rac(2) )² - (8rac(2) -2) / ( 2 - rac(2) )²

Qu'en pensez-vous ?