Dérivées. [T° ES]

par **Primdu72** » 06 Nov 2006, 21:17

Bonjour,

J'ai un exercice à faire pour le cours de Math seulement vu le piètre niveau de mon Prof et mon niveau personnel je n'y arrive pas.
Pourrais-je avoir de l'aide ?

L'intitulé est le suivant :

Soit F la fonction définie sur R-{-2} par f(x) = (X²+X-1) / (X + 2) et C sa courbe représentative dans un repère orthonormal.

1] Montrer que pour tout X appartient à R - {-2}, F(x) = X -1 + (1/X+2)

Merci de votre aide à l'avance. :we:

par **bitonio** » 06 Nov 2006, 21:28

Salut, cet exo veut te faire décomposer ta fonction en éléments plus simples:

Met X -1 + (1/X+2) au même dénominateur, et ohhh magie, ca marche :)

Bonne soirée

Ciaoo

par **Primdu72** » 06 Nov 2006, 21:38

Merci Bitonio mais mon grand frére m'a un peu expliqué et je trouve la réponse exact.

Par contre je suis encore bloqué après vu mon niveau ne valant rien.

2] Calculer les limites de F en -2
En déduire l'équation d'une droite asymptote à C.

(Toujours par rapport à l'énoncé du premier post)

par **bitonio** » 06 Nov 2006, 21:42

Alors, il y a deux limites à considérer: limite à gauche, limite à droite

F(x) = X -1 + (1/X+2)

en -2 si tu arrives par la gauche, c'est à dire x -> -2 x -2 x>2 alors1/(x+2) est positif et ....

sachant que

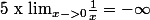
quand tu auras trouvés les limites, tu devrais avoir trouvé les asymptotes (ou plutot l'asymptote !)

Bonne chance

par **hartimer** » 06 Nov 2006, 21:55

Les explications de Bitonio manquent de quelques branlées de chiens ...

par **Primdu72** » 06 Nov 2006, 21:58

D'accord ceci est résolu.

3] Calculer les limites de F en -l'infini et en +l'infini

:hum:

par **hartimer** » 06 Nov 2006, 22:00

Cet exo est d'une lourde besogne :hum:

Dérivées. [T° ES]

Dérivées. [T° ES]

Qui est en ligne