Dérivées successives : vérification
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
par babaz » 03 Sep 2006, 16:55
Bonjour à nouveau,
Il s'agit d'exprimer
}(x))
en sachant que
 = \left(\frac{1}{x-1}\right) + \left(\frac{1}{x+1}\right))
Voilà ce que j'ai trouvé (à confirmer bien entendu) :
 = \left(\frac{- 1}{({x+1})^2}\right) - \left(\frac{1}{({x-1})^2}\right))
}(x) = \left(\frac{U_n}{(x+1)^{n+1}}\right) + \left(\frac{U_n}{(x-1)^{n+1}}\right))
avec
)
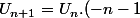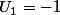
Il m'a semblé nécessaire d'intégrer ici une suite récurrente, puisqu'en calculant successivement les dérivées, il y avait effectivement un ordre logique.
Merci pour vos remarques.
PS : c'est la première fois que je m'exprime en LaTex !!!
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 03 Sep 2006, 16:57
Bonsoir
Je ne comprends pas comment tu arrives à conjecturer quelque chose après avoir seulement calculé la dérivée première ...
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
par babaz » 03 Sep 2006, 16:58
J'ai calculé plusieurs dérivées successives mais compte tenu de ma lenteur avec LaTex, il ne m'a pas semblé nécessaire de les préciser toutes.
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
par nekros » 03 Sep 2006, 17:03
Salut,
Il faut calculer plus d'une dérivée pour pouvoir conjecturer...
Tu as
=\frac{1}{x-1}+\frac{1}{x+1})
Puis
=\frac{-1}{(x-1)^2}-\frac{1}{(x+1)^2})
Puis
=\frac{2}{(x-1)^3}+\frac{2}{(x+1)^3})
Puis
=\frac{-6}{(x-1)^4}-\frac{6}{(x+1)^4})
Puis
}(x)=\frac{24}{(x-1)^5}+\frac{24}{(x+1)^5})
Tu en déduis une conjecture, que tu généralises pour tout n par récurrence.
A+
-
babaz
- Membre Naturel
- Messages: 71
- Enregistré le: 30 Aoû 2006, 15:07
-
par babaz » 03 Sep 2006, 18:11
Oui, ma ma conjecture est-elle bonne ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 03 Sep 2006, 18:24
J'aurais plutot conjecturé :
}(x)=\frac{(-1)^{n}n!}{(x-1)^{n+1}}+\frac{(-1)^{n}n!}{(x+1)^{n+1}})
:happy3:
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
par nekros » 03 Sep 2006, 18:29
Ouaip bien vu Nightmare, j'attendais la réponse de babaz...
Reste à prouver cette relation pour tout n par récurrence.
A+
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 03 Sep 2006, 18:31
Une question interressante :
A-t-on un autre moyen de preuve que la réccurence ici ?
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
