Dérivée d'une fonction trigo

par **Elda Saphira** » 24 Oct 2010, 18:17

Soit f(x) = cos(x)-cos²(x)

1) Montrer que f est 2;) périodique
2) Étudier la parité de f
3) Expliquer pourquoi on peut réduire l'étude de la courbe à l'intervalle [0;;)]
4) Résoudre l'inéquation 2cos(x)-1 > 0 sur l'intervalle [0;;)]
5) Étudier les variations de f et dresser son tableau de variation

J'ai réussi à faire les question 1 à 4 mais la 5 me pose problème

Pour étudier les variations j'ai fait la dérivée de f(x) et c'est là que j'ai dû me tromper, parce que le tableau de variation obtenu avec cette dérivée ne correspond pas à la courbe de f(x) quand je la trace sur géogébra
J'ai mis que f'(x) = -sin(x)+2sin(x) = sin(x) ; mais apparemment ce n'est pas ça :triste:

Quelqu'un aurait-il une idée de la formule à utiliser pour trouver la bonne dérivée ?
D'avance merci

par **Jimm15** » 24 Oct 2010, 18:22

Bonsoir,

et

.

par **Elda Saphira** » 24 Oct 2010, 18:35

Merci d'avoir répondu si vite !
Ce sont les formules que j'ai utiliser mais j'ai beau le refaire je trouver toujours la même chose :mur: :

f(x) = cos(x)- cos²(x)

f'(x) = -sin(x)-(-2sin(x))
= -sin(x)+2sin(x)
= sin(x)

par **Trident** » 24 Oct 2010, 18:53

f(x) = cos(x)-cos²(x)

f(x) = cos(x) - (cos(x))²

Pour tout x appartenant à [0;Pi], f'(x) = (cos(x))' - (cos(x))²

f'(x) = -sin(x) - 2(cos(x)) x (-sin(x)) = -sin(x) + 2cos(x) x sin(x).

On peut simplifier cela en factorisant par sin(x).

f'(x) = sinx ( 2cos(x) - 1 )

Voilà pour la dérivée. :lol3:

par **Jimm15** » 24 Oct 2010, 18:54

Elda Saphira a écrit:Merci d'avoir répondu si vite !
Ce sont les formules que j'ai utiliser mais j'ai beau le refaire je trouver toujours la même chose :mur: :

f(x) = cos(x)- cos²(x)

f'(x) = -sin(x)-(-2sin(x))
= -sin(x)+2sin(x)
= sin(x)

Le problème cest que

.
La dérivée de

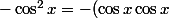vaut

.
Enfin, je pense...

par **Trident** » 24 Oct 2010, 18:56

Pour tout x appartenant à [0;Pi], f'(x) = (cos(x))' - (cos(x))²
Je voulais plutôt dire :

Pour tout x appartenant à [0;Pi], f'(x) = (cos(x))' - [(cos(x))² ]'

Et pour dériver cos²(x), j'ai utilisé le fait que [ u^n]' = nu^(n-1) x u'
Tu avais oublié le " fois u' ".

par **Elda Saphira** » 24 Oct 2010, 19:14

Merci beaucoup !!! :we:

J'aurais dû y penser*à chaque fois j'oublie de multiplier par u^(n-1)

par **Trident** » 24 Oct 2010, 19:15

De rien. ;)

Multiplier par u' plutôt. :we:

Dérivée d'une fonction trigo

Dérivée d'une fonction trigo

Qui est en ligne