Derivée term S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
zubrovska
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Oct 2007, 14:38
-
 par zubrovska » 01 Déc 2007, 16:47
par zubrovska » 01 Déc 2007, 16:47
Soit f définie sur [o; +inf[ par :
f(x)= rac(x+1)-rac(x)
b. Démontrer que f est dérivable sur ]0; + 00[ et que f' a le
même signe que -f
c. Déterminer lim f(x) (quand x tend vers +inf).
d. Déterminer lim (f(x)-1)/(x) (quand x tend vers 0 et quand x>0)
En deduire une interprétation pour Cf
e. Construire la courbe représentative de Cf dans un repère
orthonormal d'unités graphiques 2 cm.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 01 Déc 2007, 17:02
par Monsieur23 » 01 Déc 2007, 17:02
Bonjour ?
Qu'as-tu fais pour l'instant ?
« Je ne suis pas un numéro, je suis un homme libre ! »
-
zubrovska
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Oct 2007, 14:38
-
 par zubrovska » 01 Déc 2007, 17:05
par zubrovska » 01 Déc 2007, 17:05
j'ai demontré que f était positive sur 0;+inf
(question a. mais étant deja faite je ne l'ai pas énoncé ici)
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 01 Déc 2007, 17:07
par Monsieur23 » 01 Déc 2007, 17:07
Good.
Maintenant, comment tu pourrais montrer que f est dérivable ?
As-tu calculé f' ?
Une fois que tu as f', tu mets tout au même dénominateur pour trouver le résultat.
« Je ne suis pas un numéro, je suis un homme libre ! »
-
zubrovska
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Oct 2007, 14:38
-
 par zubrovska » 01 Déc 2007, 17:17
par zubrovska » 01 Déc 2007, 17:17
pour montrer que f est derivable, si je montre qu'elle est continue sur 0;+inf c'est bon non ?
je trouve pas le denominateur, ca donne (denominateur seulement): (rac(x))*(2rac(x+1) mais je n'arrive pas a develloper
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 01 Déc 2007, 17:26
par Monsieur23 » 01 Déc 2007, 17:26
Non, toutes les fonctions continues ne sont pas dérivables.
Par contre, tu sais que les fonctions

et
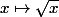
sont dérivables sur

, donc f l'est.
Tu as
 = \frac{1}{2 \sqrt{x+1}} - \frac{1}{2 \sqrt{x}})
Soit
 = \frac12 ( \frac{1}{ \sqrt{x+1}} - \frac{1}{ \sqrt{x}})
 = \frac12 ( \frac{\sqrt{x} - \sqrt{x+1}}{\sqrt{x} \sqrt{x+1}} ))
Le dénominateur est toujours positif.
« Je ne suis pas un numéro, je suis un homme libre ! »
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
