Derivée

[Edo]

Voila je viens de terminer mon bac STI :mur: :mur: et mais voila j'ai un doute sur la derivée de (lnx)²

voila ce que j'ai fait (2lnx)/x

alors si quelque peut vérifier ma dervivée :cry: :cry:

Merci

[oscar]

Bonjour



(u ²)' = 2u * u'

u = lnx

[(lnx)²]' = 2lnx * 1/x = 2 ln x / x

[bruce.ml]

Comme je le dis toujours s'il n'y a qu'une seule chose à retenir du programme de terminale c'est la composée de fonctions. Et notemment deux de ses propriétés :
avec ça on calcule TOUTES les dérivées possibles et immaginables, en conaissant juste les dérivées de , de ln, exp et des fonctions trigonométriques (j'en ai peut être oublié une ou deux ).
Deuxième utilisation TRES importante de la composée de fonction : les inéquations.
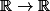Théorème : soit i une inéquation entre élements de et f une application . On a le droit de composer les deux membres de l'inéquation en toutes généralités si et seulement si la fonction f est monotone, et de deux choses l'une :
¤ la fonction f est croissante et on garde le signe de l'inégalité
¤ la fonction f est décroissante et on le signe de l'inégalité en son dual.

On peut si on le souhaite ajouter des "strictement" au théorème si l'inégalité de notre inéquation est stricte