Dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
yoopi
- Membre Naturel
- Messages: 11
- Enregistré le: 04 Fév 2007, 15:25
-
 par yoopi » 21 Fév 2007, 17:09
par yoopi » 21 Fév 2007, 17:09
Bonjour, voila on étudie les logaritmes néprériens mais pour dériver ces fonctions j'ai un peu du mal. Du coup pour mes exercices, je bloque.
J'ai justement une fonction à dériver mais avec mon problème, je n'arrive pas à trouver cette dérivée
Voici cette fonction : fn(x) = (1+nlnx)/x² sur ]0;+oo[ avec n supérieur ou égal à 2.
Merci pour votre aide .
-
maf
- Membre Rationnel
- Messages: 911
- Enregistré le: 08 Jan 2007, 17:57
-
 par maf » 21 Fév 2007, 17:16
par maf » 21 Fév 2007, 17:16
' = \frac{f'g-g'f}{g^2})
(lnx)' =
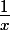
(x)' = 1
(
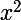
)'=2x
' = e^x)
(Attention aux domaines de définition)
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 21 Fév 2007, 17:16
par amine801 » 21 Fév 2007, 17:16
slt
si c'est bien ca ta fonction
=\frac{1+nlnx}{x^2})
alors
=\frac{\frac{n}{x}.x^2-2x.(1+nlnx)}{x^4})
=\frac{n.x-2x.(1+nlnx)}{x^4})
=\frac{n-2.(1+nlnx)}{x^3})
-
maf
- Membre Rationnel
- Messages: 911
- Enregistré le: 08 Jan 2007, 17:57
-
 par maf » 21 Fév 2007, 17:20
par maf » 21 Fév 2007, 17:20
Moi j'obtiens avec un moins ...
=\frac{n-2.(1+nlnx)}{x^3})
-
yoopi
- Membre Naturel
- Messages: 11
- Enregistré le: 04 Fév 2007, 15:25
-
 par yoopi » 21 Fév 2007, 17:33
par yoopi » 21 Fév 2007, 17:33
je trouve un moins aussi ( car la dérivée est du type u'v-uv'/v² ) . Merci de m'avoir indiqué les dérivées de chaque membre. Je crois que j'ai compris et puis avec un effort je comprendrais d'amblet..Merci
-
amine801
- Membre Rationnel
- Messages: 538
- Enregistré le: 05 Jan 2007, 18:06
-
 par amine801 » 21 Fév 2007, 17:34
par amine801 » 21 Fév 2007, 17:34
petite erreur de frape j'ai modifie
-
yoopi
- Membre Naturel
- Messages: 11
- Enregistré le: 04 Fév 2007, 15:25
-
 par yoopi » 21 Fév 2007, 17:44
par yoopi » 21 Fév 2007, 17:44
Pour résoudre l'équation f'n(x)=0, on résout le numérateur et le dénominateur séparément ?
-
maf
- Membre Rationnel
- Messages: 911
- Enregistré le: 08 Jan 2007, 17:57
-
 par maf » 21 Fév 2007, 17:45
par maf » 21 Fév 2007, 17:45
le dénominateur ne peut pas être nul !!! sinon la fonction n'existe pas ...
il faut regarder le domaine de définition de f'(x) !! ]0;+oo[ (ici idem que pour f(x), cela n'est pas tjrs le cas !!)
-
yoopi
- Membre Naturel
- Messages: 11
- Enregistré le: 04 Fév 2007, 15:25
-
 par yoopi » 21 Fév 2007, 17:51
par yoopi » 21 Fév 2007, 17:51
oui mais l'ensemble de définition n'apporte rien au problème puisque c'est l'ensemble de toute fonctions logarithmes. Je pense que tout dépend de la valeur de n mais ce dernier est supérieur ou égale à 2.
-
maf
- Membre Rationnel
- Messages: 911
- Enregistré le: 08 Jan 2007, 17:57
-
 par maf » 21 Fév 2007, 17:52
par maf » 21 Fév 2007, 17:52
ce que je voulais dire ... c'est que x^3 n'est pas égal à 0 !!! --> regarde juste le numérateur
-
yoopi
- Membre Naturel
- Messages: 11
- Enregistré le: 04 Fév 2007, 15:25
-
 par yoopi » 21 Fév 2007, 17:59
par yoopi » 21 Fév 2007, 17:59
Oui je comprends. Merci pour l'aide apportée... :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
