Dérivée TS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
kl4im
- Membre Naturel
- Messages: 47
- Enregistré le: 13 Sep 2006, 14:55
-
par kl4im » 16 Nov 2006, 18:05
Bonjour,
j'ai un dm à faire :
Soit f la fonction définie par
=\sqrt{x+\sqrt{1+x^2}})
Montrer que sa dérivée vérifie pour tout réel x :
=f(x))
J'ai donc essayé de dérivée la fonction, en considérant que
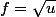
où
J'ai trouvé que
= 1 + \frac{x}{\sqrt{1+x^2}})
Je n'arrive pas à faire la suite, je ne vois pas comment m'y prendre.
Merci de me donner un coup de main.
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
par fonfon » 16 Nov 2006, 18:32
Salur, moi je change un peu la notation je prend g(x) à la place de u(x)
on a
}=\sqrt{g(x)})
avec
}=x+\sqrt{1+x^2})
on a donc
}=\frac{g^'(x)}{2\sqrt{g(x)})
or
}=1+\frac{x}{\sqrt{x^2+1}})
donc il suffit que tu remplaces g(x) et g'(x) tu obtiens f'(x)
il suffit apres de developper
})
et montrer que ça vaut f(x)
-
kl4im
- Membre Naturel
- Messages: 47
- Enregistré le: 13 Sep 2006, 14:55
-
par kl4im » 16 Nov 2006, 19:02
Alors
} = \frac{1 + \frac{x}{\sqrt{1+x^2}}}{2\sqrt{x+\sqrt{1+x^2}}} = \frac{1+x}{2\sqrt{x+\sqrt{1+x^2}}\sqrt{x^2+1}})
Peut-on transformer + ?
Est-ce correct ?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
par fonfon » 16 Nov 2006, 19:13
je te conseille de laisser
=}\frac{1+\frac{x}{\sqrt{1+x^2}}}{2\sqrt{x+\sqrt{1+x^2}}})
et de le developper avec
-
kl4im
- Membre Naturel
- Messages: 47
- Enregistré le: 13 Sep 2006, 14:55
-
par kl4im » 16 Nov 2006, 19:57
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
par fonfon » 16 Nov 2006, 20:03
on simplifie par 2 pour commencer ensuite on ecris autrement la racine carrée soit
}=\frac{(x+\sqrt{x^2+1})}{\sqrt{x+\sqrt{1+x^2}}}=\frac{(x+\sqrt{1+x^2})}{(x+\sqrt{1+x^2})^{1/2}}=(x+\sqrt{1+x^2})\times(x+\sqrt{1+x^2})^{-1/2}=...)
-
kl4im
- Membre Naturel
- Messages: 47
- Enregistré le: 13 Sep 2006, 14:55
-
par kl4im » 16 Nov 2006, 20:11
Euh...
ça doit surement faire
mais je ne vois pas trop comment développer ...
Merci beaucoup pour votre aide fonfon
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
par fonfon » 16 Nov 2006, 20:18
je ne vois pas trop comment développer ...
ben c'est simple
}=(x+\sqrt{1+x^2})(x+\sqrt(1+x^2)^{-1/2}=(x+\sqrt{1+x^2})^{2/2}(x+\sqrt{1+x^2})^{-1/2})
or
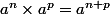
donc
}=(x+\sqrt{1+x^2})(x+\sqrt(1+x^2})^{-1/2}=(x+\sqrt{1+x^2})^{2/2}(x+\sqrt{1+x^2})^{-1/2}=(x+\sqrt{1+x^2})^{(2/2-1/2)}=(x+\sqrt{1+x^2})^{1/2}=\sqrt{x+\sqrt{1+x^2}}=f(x))
voilà A+
-
kl4im
- Membre Naturel
- Messages: 47
- Enregistré le: 13 Sep 2006, 14:55
-
par kl4im » 16 Nov 2006, 20:40
Dsl mais ce n'est pas fini ...
Je dois maintenant en déduire que le dérivée seconde de f vérifie
f"(x)+4xf'(x)-f(x)=0)
Alors j'ai trouvé que
![](https://latex.ilemaths.net/ile_TEX.cgi?f"(x)=\large\frac{\sqrt{x^2+1}-x^2}{(x^2+1)\sqrt{x^2+1}})
Donc
f"(x)+4xf'(x)-f(x))
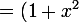\frac{\sqrt{x^2+1}-x^2}{(x^2+1)\sqrt{x^2+1}}+4x(1+\frac{x}{\sqrt{x^2+1}})-\sqrt{x+\sqrt{1+x^2}})
\sqrt{x^2+1}}+4x+\frac{4x^2}{\sqrt{x^2+1}}-\sqrt{x+\sqrt{1+x^2}})
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
par fonfon » 16 Nov 2006, 21:31
Re,
tu sais que :
=\sqrt{x^2+1}f'(x))
donc
=\frac{f(x)}{\sqrt{x^2+1}})
donc
=\frac{f'(x)}{2\sqrt{1+x^2}}+\frac{xf(x)}{2(x^2+1)\sqrt{x^2+1}}=....)
(remplaces encore f'(x))
donc remplaces et regardes ce que ça fait
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
par fonfon » 17 Nov 2006, 08:21
Salut,
il vaut mieux faire en utilisant ce qu'on te donne soit:
tu sais que
}=2\sqrt{1+x^2}f'(x))
donc
}=\frac{2x}{\sqrt{1+x^2}}f'(x)+2\sqrt{x^2+1}f^{''}(x))
donc
}=\frac{f'(x)}{2\sqrt{x^2+1}}-\frac{xf'(x)}{x^2+1})
et maintenant tu remplaces dans
f^{''}(x)+4xf'(x)-f(x))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
