DM dérivée

[Anonyme]

Salut a tous,
voilà je suis en terminale S et j'ai un problème avec un DM.

Il faut que je trouve la dérivée de cette fonction:
f(x)= 1-x / x²+1.
Ensuite il faut que j'en déduise le tableau de variation.

Pour la dérivée, j'ai trouvée f'(x)= x²-2x-1 / (x²+1)²
Est-ce que c'est ça???

Ensuite, je ne vois pas trop comment faire pour le tableau de variation pouvez-vous m'indiquer la démarche s'ils vous plait?

[Kovalle]

Bonjour,

Ta dérivée est juste.

Maintenant tu dois étudier le signe de ta dérivée sur son ensemble de définition. Pour cela étudie le signe du numérateur, et le dénominateur. (à l'aide d'un tableau de signe).

Ensuite, en fonction du signe de la dérivée sur son ensemble de définition, tu en déduis les variations de ta fonction de départ.
(Exemple: Si f'(x) négative sur I alors f(x) décroissante sur I (ou I est un intervalle) et vice versa avec f'(x) positive)

[Anonyme]

Merci, c'est gentil de me répondre :)

Pour le numérateur, je dois utiliser delta vu qu'il s'agit d'une fonction polynôme du second degré mais je trouve deux racines distinctes assez bizarre:
je trouve x1= 2-racine de 8 / 2
et pour x2: 2+ racine de 8/2
quand je verifie a la calculatrice sur la courbe ça ne correspond pas du tout! :/

[Kovalle]

On a le polynôme suivant x²-2x-1

Donc 2 solutions:





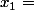
Tes racines sont justes, tu en déduis que comme le coefficient de x² est positif, alors le polynôme (ton numérateur) est positif à l'extérieur des racines. C'est à dire sur et sur

De plus, le dénominateur de ta dérivée est toujours strictement positif. Donc en faisant un tableau de signe tu dois trouver que ta dérivée est positive sur et sur et donc que ta fonction est croissante sur ce même intervalle.
Et est décroissante sur

[Anonyme]

Merci pour votre réponse :p

Ensuite j'ai du déterminer la tangente T à f(x), j'ai trouvé y=-0,5x+0,5 :)

Mais maintenant je dois déterminer les positions relatives de f(x) et y!

Faut-il que je fasse: f(x)-y= (1-x)/(x²+1) - (-0,5x+0,5)
Car je ne vois pas trop l’intérêt! :/

De plus c'est écrit: "on pourra démontrer que x^3-x²-x+1=(x-1)²(x+1)

Je suis complètement embrouiller :(

[LeFish]

Oui : pour déterminer les positions relatives, il faut étudier le signe de f(x) - y. Si c'est positif, ta fonction f est au dessus de T, si c'est nul, elles sont confondues, si c'est négatif, T est au dessus de f.

[Anonyme]

Merci, mais dans c'est cas là, a quoi sert la derniere phrase: "on pourra démontrer que x^3-x²-x+1=(x-1)²(x+1)"

De plus, je ne vois pas trop comment faire quand je suis a:
f(x)-y= (1-x)/(x²+1) + 0,5x - 0,5
Faut-il tout mettre au même dénominateur??

[LeFish]

Ouioui, il faut faire ça.

Aussi, ne te demande pas à quoi sert une phrase ! Si tu en auras besoin pendant l'exercice, tu l'utiliseras.
Si tu as fini touuut l'exercice et que tu ne l'as pas utilisée, soit tu es très fort, soit tu t'es trompé.

[Anonyme]

Ouioui, il faut faire ça.

Aussi, ne te demande pas à quoi sert une phrase ! Si tu en auras besoin pendant l'exercice, tu l'utiliseras.
Si tu as fini touuut l'exercice et que tu ne l'as pas utilisée, soit tu es très fort, soit tu t'es trompé.

Bah j'ai du me tromper...
je comprend pas j'arrive à:
f(x)-y= 0,5x^3-0,5x²-1,5x+1,5 / x²-1

C'est bizarre non?

[LeFish]

Tu es sûr que tu ne t'es pas trompé pour déterminer l'équation de la tangente T ?

[Anonyme]

Tu es sûr que tu ne t'es pas trompé pour déterminer l'équation de la tangente T ?

bah je sais pas...
L'équation de la tangente a la courbe representative de f au point A d'abscisse 1 est égale à:
y=f'(1)(x-1)+f(1)

f'(1)= x²-2x-1 / (x²+1)² = 1-2-1 / 4 = -2/4 = -0,5
f(1)= 1-x / x²+1 = 0

y= -0,5 (x-1) +0 y -0,5x+0x5

[LeFish]

Tu t'es trompé quand tu as calculé f(x) - y , j'ai vu où était ton erreur.
Normalement tu pourras factoriser par 0,5 et utiliser l'indication !

[Anonyme]

Tu t'es trompé quand tu as calculé f(x) - y , j'ai vu où était ton erreur.
Normalement tu pourras factoriser par 0,5 et utiliser l'indication !

Peux-tu me préciser de quel erreur il s'agit s'il te plait...
ça fait longtemps que je cherche

[LeFish]

Tu devrais trouver !

[Anonyme]

tu as réussi a trouver ça avec mes valeurs?
Car quand je relis mon calcul, il n'y a pas d'erreurs de signes ni de calculs...

Ma tangente est bien correcte?

[LeFish]

Ta tangente est correcte.
Fais attention au signe des termes en x et des termes constants !

Normalement au numérateur (j'ai la flemme d'écrire le dénominateur) tu dois avoir

[Anonyme]

Un énorme merci! :)) j'ai réussi a comprendre mon erreur...
Au lieu de diviser le tout par x²+1, je divisais et multipliais les numérateurs par x²-1 d'où mon problème de signe ;p

[Anonyme]

Ta tangente est correcte.
Fais attention au signe des termes en x et des termes constants !

Normalement au numérateur (j'ai la flemme d'écrire le dénominateur) tu dois avoir

Merci, je me retrouve avec :
= 0,5 (x^3-x²-x+1) / x²+1
= 0,5 ( (x-1)² (x+1) ) / x²+1

Maintenant, je peux continuer a developper, ou je peux directement étudier le signe de f(x)-y??

Sinon, ça me donne
= 0,5 ( (x²-2x+1) (x+1) / x²+1 (je supprime les termes communs)
= 0,5 ( -2x(x+1) )
= 0,5 ( -2x²-2x )
= -x²-x

[LeFish]

Ah non, tu ne peux pas supprimer les termes communs !!
On peut le faire que dans ce cas là : !

Tu ne peux pas simplifier de cette façon là ! Vu qu'au numérateur tu as x²-2x+1 ! Si tu avais x²+1 à la place, là tu aurais pu supprimer ces termes !

Du coup, ne continue pas à développer et étudie directement le signe de f(x)-y !