Derivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Fraise-acide
- Membre Naturel
- Messages: 40
- Enregistré le: 20 Jan 2010, 15:41
-
 par Fraise-acide » 21 Avr 2010, 17:50
par Fraise-acide » 21 Avr 2010, 17:50
en dérivant e^-x (1-x ) + 1
avec la formule u'v+uv' je trouve f' = -e^x + e^-2x - e^-x
jene sais pas comment simplifier...
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 21 Avr 2010, 17:53
par gigamesh » 21 Avr 2010, 17:53
Bonjour,
ta fonction c'est
 +1)
ou bien
} +1)
ou bien ... ?
-
Fraise-acide
- Membre Naturel
- Messages: 40
- Enregistré le: 20 Jan 2010, 15:41
-
 par Fraise-acide » 21 Avr 2010, 18:12
par Fraise-acide » 21 Avr 2010, 18:12
il me semble que c'est faux non ?
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 21 Avr 2010, 18:17
par gigamesh » 21 Avr 2010, 18:17
Alors ta fonction c'est uv+1 avec
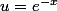
et
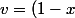)
donc

et
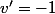
et ta dérivée est incorrecte ;
une fois que tu auras corrigé l'erreur, tu pourras mettre l'exponentielle en facteur (et une exponentielle c'est strictement positif, ce qui devrait bien nous aider pour étudier le signe de la dérivée)
-
loriane007
- Messages: 6
- Enregistré le: 21 Avr 2010, 12:04
-
 par loriane007 » 21 Avr 2010, 18:20
par loriane007 » 21 Avr 2010, 18:20
quand tu applique ta formule e u'v+uv' ne distribue pas ton
)
comme ça après tu factorise par
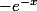
-
Fraise-acide
- Membre Naturel
- Messages: 40
- Enregistré le: 20 Jan 2010, 15:41
-
 par Fraise-acide » 21 Avr 2010, 18:27
par Fraise-acide » 21 Avr 2010, 18:27
u'v + uv'
= -e^-x (1-x) + e^-x*(-1)
= -e^-x - (-e^-x *x) -e^-x
= -e^-x + e^-2x -e^-x
????
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 21 Avr 2010, 18:36
par gigamesh » 21 Avr 2010, 18:36
Fraise-acide a écrit:u'v + uv'
= -e^-x (1-x) + e^-x*(-1)
oui
Fraise-acide a écrit:= -e^-x - (-e^-x *x) -e^-x
oui
Fraise-acide a écrit:= -e^-x + e^-2x -e^-x
????
non non non
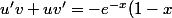+e^{-x}(-1)=e^{-x}(-(1-x)-1)=e^{-x}(x-2))
qui est du signe de x-2 vu que l'expo est positive
Attention !!!!

ce n'est pas
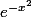
ni

-
Fraise-acide
- Membre Naturel
- Messages: 40
- Enregistré le: 20 Jan 2010, 15:41
-
 par Fraise-acide » 21 Avr 2010, 18:47
par Fraise-acide » 21 Avr 2010, 18:47
Je vois...
e^-x * x = 2e^-x
et pour le tableau de variation :
0 2 +inf
e^-x +
x-2 - 0 +
-
Fraise-acide
- Membre Naturel
- Messages: 40
- Enregistré le: 20 Jan 2010, 15:41
-
 par Fraise-acide » 21 Avr 2010, 18:49
par Fraise-acide » 21 Avr 2010, 18:49
.......0............2.................... +inf
e^-x..................... +
x-2....... -.......0......+
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 21 Avr 2010, 18:57
par gigamesh » 21 Avr 2010, 18:57
Fraise-acide a écrit:Je vois...
e^-x * x = 2e^-x
euh la non pas du tout aïe aïe aïe !

Je pense que tu confonds avec
^2=e^{2x})
qu'on utilise pour résoudre des équations du genre

en les réécrivant

avec
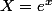
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 21 Avr 2010, 18:58
par gigamesh » 21 Avr 2010, 18:58
Mais OK pour le tableau de signes ; juste une question : pourquoi commences-tu à x=0 ? L'énoncé dit que la fonction est définie sur [0;+inf[ ?
-
Fraise-acide
- Membre Naturel
- Messages: 40
- Enregistré le: 20 Jan 2010, 15:41
-
 par Fraise-acide » 21 Avr 2010, 19:07
par Fraise-acide » 21 Avr 2010, 19:07
non. Alors x = -inf.............0.......2.........+inf
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 21 Avr 2010, 19:15
par gigamesh » 21 Avr 2010, 19:15
Ouaip.
Et ta fonction est décroissante sur ]-inf ; 2] puis croissante sur [2 ; +inf [.
Elle a donc un minimum atteint en 2.
Il n'y a plus qu'à trouver les limites ...
-
Fraise-acide
- Membre Naturel
- Messages: 40
- Enregistré le: 20 Jan 2010, 15:41
-
 par Fraise-acide » 21 Avr 2010, 19:25
par Fraise-acide » 21 Avr 2010, 19:25
Génial. Il y a un 0 en x=1 non ? Et puis le minimum en x = 2 soit en f(x) = 0.
Les limites ne sont pas demandées, et au pire je les ai.
Ensuite, en calculant la dérivée de g(x)= x((e^-x) +1)
j'ai trouvé g' = 1(e^-xe^-x) = 2e^-2x.
Et le TV est positif / croissant sur - à + infini.
-
Fraise-acide
- Membre Naturel
- Messages: 40
- Enregistré le: 20 Jan 2010, 15:41
-
 par Fraise-acide » 21 Avr 2010, 19:36
par Fraise-acide » 21 Avr 2010, 19:36
et voilà et voilà ! Plus personne ne veut m'aider.
-
Fraise-acide
- Membre Naturel
- Messages: 40
- Enregistré le: 20 Jan 2010, 15:41
-
 par Fraise-acide » 21 Avr 2010, 19:38
par Fraise-acide » 21 Avr 2010, 19:38
"oh non elle a encore une fonction à dériver celle-là ! Déjà qu'on a mit une heure à lui expliquer la première..."
et j'ai encore des tonnes d'autre questions de TaleES si vous voulez savoir..
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 21 Avr 2010, 19:42
par gigamesh » 21 Avr 2010, 19:42
Il n'y avait pas un +1 dans l'expression de départ ?
alors pour x=1 on a
+1=e^{-1}(1-1)+1=e^{-1}.0+1=1)
Et le minimum est

atteint en 2 ; ce minimum est positif car on a -20[/TEX]
Donc pas de zéros... La fonction f ne prend que des valeurs strictement positives.
Pour ta fonction g, on a g'=f>0 donc g est strictement croissante.
Explique moi comment tu as fait pour trouver que g'(x) = 1(e^-xe^-x) = 2e^-2x ???
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 21 Avr 2010, 19:44
par gigamesh » 21 Avr 2010, 19:44
Mais c'est que tu es susceptible dis donc !!
En fait il se trouve que j'ai des Tale ES donc je pourrais leur replacer tes exos héhé :we:
Donc vas-y envoie des fonctions à étudier, ça ne me fait pas peur !
-
Fraise-acide
- Membre Naturel
- Messages: 40
- Enregistré le: 20 Jan 2010, 15:41
-
 par Fraise-acide » 21 Avr 2010, 20:07
par Fraise-acide » 21 Avr 2010, 20:07
Très bien, mais tu vas avoir du fil à retordre.. : )
g(x) = x((e^-x) +1)
-> uv. u = x u' = 1, v = ((e^-x) +1) v' = -e^-x
g' = 1((e^-x) +1) + x-e^-x = x2e^-x + 1
Au fait, je dois déduire le signe de f(x) pour tout x réel, et ensuite déterminer le tableau de variation de g à partir de cette réponse.
Aussi, je dois chercher la tangente au point d'abscisse 0 de g -> T0= g(0)(x-0)+g'(0)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
+1=e^{-1}(1-1)+1=e^{-1}.0+1=1)
 atteint en 2 ; ce minimum est positif car on a -20[/TEX]
atteint en 2 ; ce minimum est positif car on a -20[/TEX]