Dérivée Petit exercice Aide S.V.P.

[jeansuce]

J'ai la dérivée suivante: 5/3fois racine de x donc au dessus 5 et en dessous 3 fois racine de x et j'ai trouver 1/6fois x fois racine de x , est ce que quelqu'un peut m'aider car si je me trompe maintenant je risque de me tromper pour les exercices suivants?
Merci d'avance!

[sara97]

C'est quoi exactement la question ?

[paquito]

Est que c'est parce que dans ce cas .

[Robic]

Ben non, c'est « 5/3 fois racine de x ».

Donc la dérivée, c'est 5/3 fois (1 sur 2 racine de x) ce qui fait dans les .

[jeansuce]

en gros c'est 5 au nominateur et le produit 3 fois racine carré de x

[jeansuce]

et je voudrais juste la réponse pour vérifier la mienne comme ça je comprends dès le début

[jeansuce]

j'ai trouver 1/ 6fois x fois racine carré de x

[Robic]

Ah, j'ai compris, c'est !

Sois précis quand tu décris une fonction et ajoute des parenthèses ! 5/3 fois racine de x, normalement ça signifie qu'on fait 5/3 multiplié par racine de x, sinon on écrit 5 divisé par (3 racine de x).

Si tu ne veux pas utiliser les balises tex, écris au moins la formule sous la forme : 5 / (3 Vx).

(Attention aussi au vocabulaire : « nominateur » n'existe pas et on se demande s'il s'agit du numérateur ou du dénominateur...)

Bref, je calcule la dérivée et je te dis si c'est bon... Voilà, c'est fait, et je trouve : .

[jeansuce]

Ok merci je vais voir où j'ai fait l'erreur sinon merci pour la réponse , merci bcp

[jeansuce]

J'ai un problème j'ai trouvé nominateur: 5 dénominateur 18fois x fois racine de x
peux tu recalculer stp pour savoir qui c'est trompé? Merci d'avance

[Robic]

J'ai vérifié, mon calcul a l'air bon. Peux-tu détailler ton calcul ici ?

(Tu ne peux pas utiliser les touches / et (), ce serait plus lisible ? Ex: 5 / (18 x Vx) À moins que tu aies un clavier limité ?)

[jeansuce]

Voilà je trouve 5/(18xVx) et j'aimerais bien connaître ta démarche pour savoir ou je me suis trompé

[Robic]

Peux-tu détailler ton calcul ici ? (Pour savoir où tu t'es trompé.)

[jeansuce]

ça va être dur de détailler mais en gros j'ai utiliser la formule dérivé de (a/b) au début ça donne -5 fois dérivé de (3Vx) sur (dénominateur) racine carré de 3Vx

[Robic]

Dans la formule (a/b), tu choisis quoi pour a et quoi pour b ? Et tu obtiens quoi pour a' et quoi pour b' ?

N'aies pas peur de montrer un calcul faux, le but est juste de trouver l'erreur.

[paquito]

Si on utilise ta méthode, on trouve: ; il y a une simplification par 3 que tu as dû louper!
Sinon, on peut écrire et , ce qui donne le résultat car x^3/2=xVx.

[jeansuce]

Merci beaucoup ! C'est bien la simplification par trois que j'ai pas fait du coup j'avais des chiffres trop grands Merci paquito et Robic ! :D

[jeansuce]

Je viens de trouver -5/6xVx je m'étais bien trompé merci ! Merci encore.... Merci!!!!

[Robic]

La méthode consistant à dériver a/b n'est en fait pas judicieuse puisqu'ici a est juste une constante.

La méthode que je préfère dans ce cas, c'est celle qu'a montré Paquito avec la puissance -1/2. Mais il paraît qu'on ne voit plus, au lycée, le fait que .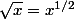

Du coup, je pense que la « bonne » méthode (dans le contexte d'un cours de lycée), c'est de poser et de dire que la fonction est de la forme , donc sa dérivée est de la forme . Reste à calculer u' : d'après le tableau des dérivées usuelles.

(En fin de compte ça ne fait pas vraiment gagner du temps par rapport à la dérivée de a/b...)

[jeansuce]

Si justement mon prof emploie ce style de méthodes mais je ne me suis pas encore assez exercé pour savoir lorsqu'il est mieux de mettre les racines ou les exposants. Maintenant avec ce que tu as dit il est vrai que ayant une constante faire la dérivée de x aurait été plus simple plus tôt que de passer par maintes formules comme je l'ai fais car plus la formule est longue plus il y a de chances qu'on fasse une erreur!