Dérivée à la dérive

[Ced111]

Bonjour,

Voilà je butte sur une dérivée

f(x) = x * sin(3x + pi/5)

J'ai fait ainsi:

g(x)= x
g'(x)= 1
h(x)= sin
h'(x)= cos
i(x)=(3x + pi/5)
i'(x)= 3

donc cela donne:

1* sin(3x +pi/5) + x * 3cos (3x + pi/5)


En fait, je ne sais pas s'il y a moyen de dériver pi/5. Comme il n'est pas multiplié par x, je suppose qu'il ne peut être dérivé.

Merci par avance pour la réponse :livre:

[L.A.]

Bonsoir,

ta dérivée est bonne, quant au pi/5 c'est une constante, sa dérivée est nulle (la dérivée d'une fonction affine f(x)=ax+b est toujours une fonction constante f'(x)=a).

[Ced111]

Un grand merci à toi et bonne nuit ;)

[tototo]

Bonjour,

Voilà je butte sur une dérivée

f(x) = x * sin(3x + pi/5)

U(x)=x
V(x)=sin(3x+pi/5)

f'(x)=1*sin(3x+pi/5)+x*3cos(3x+pi/5)
=sin(3x+pi/5)+3xcos(3x+pi/5)


J'ai fait ainsi:

g(x)= x
g'(x)= 1
h(x)= sin
h'(x)= cos
i(x)=(3x + pi/5)
i'(x)= 3

donc cela donne:

1* sin(3x +pi/5) + x * 3cos (3x + pi/5)


En fait, je ne sais pas s'il y a moyen de dériver pi/5. Comme il n'est pas multiplié par x, je suppose qu'il ne peut être dérivé.

Merci par avance pour la réponse :livre:[/quote]

[Axiom]

Bonjour tototo,

Soit

Tu as tout à fait raison et ta dérivée est correcte :lol3:
Il s'agit ici à la fois d'une dérivée de fonction composée et d'un produit.
La dérivée d'une fonction composée (Type sinus, cosinus, ou même une fonction par exemple) est ainsi :

Le produit de deux fonctions se dérive quant à lui :


Ici, tu as donc en posant :

et

Dans la dérivée de ce qui correspond à ton , c'est et comme l'a précisé L.A. plus haut, une constante (comme 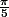) a pour dérivée 0, ce qui explique que tu ne retrouves que 3 en tant que dérivée de ici.

Tu appliques ensuite la dérivée du produit :


Voilà... :happy:

[Ced111]

Merci Axiom

Un très bel été à toi ;)

[tototo]

Bonjour

Je n'avais pas preciser les etapes vous avez raisin axiom...