Dérivé de logarithme
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
captainmath
- Membre Naturel
- Messages: 15
- Enregistré le: 18 Mar 2014, 21:32
-
 par captainmath » 10 Nov 2014, 17:17
par captainmath » 10 Nov 2014, 17:17
Bonjour,
j'ai un exo que mon prof de math m'a donné en supplément mais je suis complètement bloqué au début


Exo: log
acos1/a^sinx
Ce que j'ai fait:
(cos1/a^sinx)'/(cos1/a^sinx.lna)
Mercii à ceux qui m'aideront :lol3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Nov 2014, 17:39
par Ben314 » 10 Nov 2014, 17:39
Salut,
a) Peut tu taper ta fonction en
MimeTeX ou au moins mettre des parenthèses (çi possible au bon endroit...) pour qu'on y comprenne quelque chose.
b) oukèlé la question ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
captainmath
- Membre Naturel
- Messages: 15
- Enregistré le: 18 Mar 2014, 21:32
-
 par captainmath » 10 Nov 2014, 18:10
par captainmath » 10 Nov 2014, 18:10
Voila l'exercice:
[img]http://latex.codecogs.com/gif.latex?log_{a}cos\frac{\1}{\&space;a^{sinx}}[/img]
Mercii de ton aide :lol3:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Nov 2014, 18:33
par Carpate » 10 Nov 2014, 18:33
captainmath a écrit:Voila l'exercice:
[img]http://latex.codecogs.com/gif.latex?log_{a}cos\frac{\1}{\&space;a^{sinx}}[/img]
Mercii de ton aide :lol3:
=log_{a(}\frac{1}{a^{sinx}}))
Tu pourrais passer à la forme :
=-log_{a}(a^{sinx})=-log_{a}(e^{sinx.loga}))
sachant que
]'=\frac{1}{xlog_{a})
-
captainmath
- Membre Naturel
- Messages: 15
- Enregistré le: 18 Mar 2014, 21:32
-
 par captainmath » 10 Nov 2014, 18:50
par captainmath » 10 Nov 2014, 18:50
Carpate a écrit:=log_{a(}\frac{1}{a^{sinx}}))
Tu pourrais passer à la forme :
=-log_{a}(a^{sinx})=-log_{a}(e^{sinx.loga}))
sachant que
]'=\frac{1}{xlog_{a})
Le calcul ne serait-il pas encore plus compliqué après ça ???:hein2:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Nov 2014, 18:51
par Carpate » 10 Nov 2014, 18:51
captainmath a écrit:Le calcul ne serait-il pas encore plus compliqué après ça ???:hein2:
Je suis vraiment aller chercher des complications !
=\frac{1}{{sinx})
-
captainmath
- Membre Naturel
- Messages: 15
- Enregistré le: 18 Mar 2014, 21:32
-
 par captainmath » 10 Nov 2014, 19:07
par captainmath » 10 Nov 2014, 19:07
Carpate a écrit:Je suis vraiment aller chercher des complications !
=\frac{1}{{sinx})
Excuse moi mais es tu sur que se soit possible ?? :hein: comment es tu arrivé à cette conclusion ???
Mercii de ton aide
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 10 Nov 2014, 19:39
par Carpate » 10 Nov 2014, 19:39
captainmath a écrit:Excuse moi mais es tu sur que se soit possible ?? :hein: comment es tu arrivé à cette conclusion ???
Mercii de ton aide
}=x)
}=e^{ln(x)}=x)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 10 Nov 2014, 23:06
par Ben314 » 10 Nov 2014, 23:06
Sauf que, la formule que je lit sur le confetti (:zen:) fourni gracieusement par
captainmath, ça me semble être
\Big))
ça se simplifie (un tout petit peu) en
\Big))
mais après...
@carpate : en plus du cosinus qui est trop petit pour que tu l'ai lu, perso, je vois plutôt du

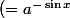\)
que du

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
captainmath
- Membre Naturel
- Messages: 15
- Enregistré le: 18 Mar 2014, 21:32
-
 par captainmath » 11 Nov 2014, 13:42
par captainmath » 11 Nov 2014, 13:42
Ben314 a écrit:Sauf que, la formule que je lit sur le confetti (:zen:) fourni gracieusement par
captainmath, ça me semble être
\Big))
ça se simplifie (un tout petit peu) en
\Big))
mais après...
@carpate : en plus du cosinus qui est trop petit pour que tu l'ai lu, perso, je vois plutôt du

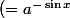\)
que du

Tu as tout a fait raison :we: je n'ai pas vu que @Carpate avait mal compris :id:
Est ce que le calcul est plus dur comme ça ???

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Nov 2014, 14:10
par Ben314 » 11 Nov 2014, 14:10
Ben il ne me semble pas que ça se simplifie plus donc, pour calculer la dérivée du bidule, il faut "enquiller" trois fois la formule de dérivation d'une composée...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
captainmath
- Membre Naturel
- Messages: 15
- Enregistré le: 18 Mar 2014, 21:32
-
 par captainmath » 11 Nov 2014, 16:54
par captainmath » 11 Nov 2014, 16:54
Je voudrais etre sur d'avoir la bonne réponse est ce que quelqu'un peut il m'aider ?????


Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
que du