Dérivation - Utilité du taux d'acroissement et de la limite

[sakuratsu]

[FONT=Georgia]Bonsoir,


Étant en train de réviser le chapitre sur la dérivation en 1S, je remarque que calculer le taux d’accroissement lorsque h tend vers 0 pour une fonction f, revient au même que d'appliquer les propriétés des fonctions dérivées de référence.

Exemple


Soit la fonction f définie par f(x) = 7*(x^2) - 6 définie sur IR, dérivable en a de IR.

Si l'on applique les propriétés des fonctions dérivées de référence, on a :


f'(a) = 7*(2a)
f'(a) = 14a.


Si l'on calcule le taux d'accroissement tel que h tend vers 0, on a :

f'(a) = 7*(a^2) - 6 = 7(a^2) - 6
f'(a + h) = 7(a^2) + 14ah + 7(h^2) - 6

f'(a + h) - f'(a) = 7(h^2) + 14ah.

Le taux d'accroissement vaut donc :

[ 7(h^2) + 14ah ] / h

[ f'(a + h) - f'(a) ] / h = 7h + 14a.

La limite du taux d'accroissement lorsque h tend vers 0 vaut donc 14a.


On retrouve le même résultat que précédemment.

Alors, pour démontrer, par exemple, que la dérivée de la fonction carrée est f(x) = 2x, peut-on calculer le taux d'accroissement tel que h tend vers 0 ?



Bonne soirée,
Sakura.[/FONT]

[mathelot]

[FONT=Georgia]Bonsoir,


Étant en train de réviser le chapitre sur la dérivation en 1S, je remarque que calculer le taux d’accroissement lorsque h tend vers 0 pour une fonction f, revient au même que d'appliquer les propriétés des fonctions dérivées de référence.

Exemple


Soit la fonction f définie par f(x) = 7*(x^2) - 6 définie sur IR, dérivable en a de IR.

Si l'on applique les propriétés des fonctions dérivées de référence, on a :


f'(a) = 7*(2a)
f'(a) = 14a.


Si l'on calcule le taux d'accroissement tel que h tend vers 0, on a :

f'(a) = 7*(a^2) - 6 = 7(a^2) - 6
f'(a + h) = 7(a^2) + 14ah + 7(h^2) - 6

f'(a + h) - f'(a) = 7(h^2) + 14ah.

Le taux d'accroissement vaut donc :

[ 7(h^2) + 14ah ] / h

[ f'(a + h) - f'(a) ] / h = 7h + 14a.

La limite du taux d'accroissement lorsque h tend vers 0 vaut donc 14a.


On retrouve le même résultat que précédemment.

Alors, pour démontrer, par exemple, que la dérivée de la fonction carrée est f(x) = 2x, peut-on calculer le taux d'accroissement tel que h tend vers 0 ?



Bonne soirée,
Sakura.[/FONT]

oui.......................

[LonelyGuy]

J'avais remarqué exactement la même chose que toi et dans un exercice je me rappelle qu'il était justement demandé d'utiliser les deux méthodes ! Cela revient donc exactement au même ! Oui.

[Grimmys]

Je ne voudrais pas dire de connerie, car je suis moi même en 1erS, mais l'utilité du taux d’accroissement peut peut-être se trouver dans le cas où nous n'avons pas des fonctions de référence, non ?

[capitaine nuggets]

Salut !

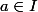En fait c'est une définition : une fonction définie sur un intervalle ouvert est dérivable en , si le taux d'accroissement admet une limite finie lorsque tend vers et dans ce cas, on note le nombre dérivé de au point d'abscisse :+++:

Revenir à la définition peut parfois être utile quand on a des fonctions exprimées par morceaux, ou sur des bords du domaine de définition, ou ...
Montrer par exemple que la fonction définie pour tout réel non nul par et est dérivable quel que soit x.
On peut directement affirmer que est au moins dérivable sur et sur . Le problème se pose en où il faut revenir à la définition en calculant la limite du taux d'accroissement en :+++:

[mathelot]

?? ........................

[capitaine nuggets]

Oui, au départ, j'avais mis des limites, puis je les ai enlevées pour placer "taux d'accroissement", je corrige :++:

[Joker62]

Hello,

La question essentielle est :
Quand tu veux te faire cuire des pâtes, est-ce-que tu fais pousser un champ de blé avant ?

Pour la dérivation c'est pareil :
Le taux d'accroissement sert à calculer la dérivée des fonctions de base (Fonction affine, fonction carrée, fonction inverse etc...)
Ensuite viennent les théorèmes : Si on multiplie une fonction par une constante, alors sa dérivée est multipliée par la même constante etc...
Cette recette permet d'accélérer les choses :

Pour dériver la fonction f : x -> 7x^2 + 4x - 3 on remarque qu'il y a du x^2 que l'on multiplie par une constante et une fonction affine.
On a f'(x) = 7*2x + 4 que l'on obtient avec les théorèmes (et derrière les théorèmes il y a du taux d'accroissement)

[zygomatique]

salut

revenons à une interprétation géométrique ::

1/ qu'est qu'un taux de variation (ou d'accroissement) d'une fonction f entre deux points de sa courbe représentative ?

2/ que se passe-t-il si l'un des points se rapproche indéfiniment de l'autre (fixe) (quand un point tend vers l'autre) ?

3/ quelle est la définition du nombre dérivé ?

Étant en train de réviser le chapitre sur la dérivation en 1S, ....

je ne sais si tu es déjà en première S .... mais avant de réviser il faut déjà viser ....

[sakuratsu]

Merci Mathelot.

Je pense avoir eu ma réponse.

[mathelot]

Merci Mathelot.

Je pense avoir eu ma réponse.

une appli moins connue du taux d'accroissement:

soit

f est continue en tous points. Pour montrer qu'elle n'est dérivable en aucun point on forme le taux


et on montre qu'il n'est pas majoré pour des bien choisis
et tendant vers zéro.

[Joker62]

mathelot tu picoles un peu trop