Dérivation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 25 Fév 2013, 19:43
par Anthony666 » 25 Fév 2013, 19:43
On considère la fonction f définie sur [-3,3] par : f(x)= x²-2x-3.
On appelle P sa courbe représentative dans un repère orthonormé (unité: 1cm).
1)a) Calculer f'(x) où f' est la dérivée de f.
b) Etudier le signe de f'(x).
c) En déduire les variations de la fonction f et donner son tableau de variation.
d) Déterminer l'extremum de la fonction f.
2)a) Déterminer les coordonnées des points A1 et A2 où la parabole P coupe l'axe des abscisses.
b) Tracer les tangentes T1 et T2 à P aux points A1 et A2.
3) Tracer la parabole P.
4) Déterminer une équation de chacune des tangentes T1 et T2.
Merci de bien vouloir répondre à mon exercice s'il vous plait ( sachant que j'ai déjà répondus jusqu'a la question 2)a)
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 25 Fév 2013, 20:50
par Cheche » 25 Fév 2013, 20:50
Bonsoir Anthony :):)
Tu peux nous énoncer tes réponses jusqu'à la question 2a plz.
Pour voir où tu en es ?
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 25 Fév 2013, 20:53
par Cheche » 25 Fév 2013, 20:53
Rappel :
L'équation de la tangente

à la courbe f au point d'abscisse a est :
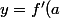 (x-a) + f(a))
En effet,
- le coefficient directeur de

est bien
)
.
- le point
 ) \in T)
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 26 Fév 2013, 00:09
par Anthony666 » 26 Fév 2013, 00:09
1)a) 2x-2
b) sur [-3,1] négatif et sur [1,3] positif
c) dévroissante puis croissante
d) le minimum est -4 pour x=1
 par thismeanswar » 26 Fév 2013, 08:10
par thismeanswar » 26 Fév 2013, 08:10
y = f'(a) (x-a) + f(a)
En effet,
- le coefficient directeur de T est bien f'(a).
- le point (a ; f(a) ) \in T
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 26 Fév 2013, 09:08
par Cheche » 26 Fév 2013, 09:08
alors avec mon aide, tu en es où ?
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 26 Fév 2013, 14:18
par Anthony666 » 26 Fév 2013, 14:18
2)a) A1(-1,0)
A2(3,0)
A la question 2)b) je suis coincé

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 26 Fév 2013, 14:22
par ampholyte » 26 Fév 2013, 14:22
Bonjour,
Tu dois calculer la tangente T1 en -1 et la tangente T2 en 3
Méthode :
- Calculer f'(x)
- Utiliser la formule de la tangente : y = f'(a)(x - a) + f(a)
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 26 Fév 2013, 14:35
par Anthony666 » 26 Fév 2013, 14:35
votre formule c'est la même que celle la : y=f'(xA)(x-xA)+yA ? Car j'ai cette formule dans mon cours
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 26 Fév 2013, 14:41
par Anthony666 » 26 Fév 2013, 14:41
J'arrive pas a calculer je comprends rien a la formule !

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 26 Fév 2013, 14:46
par ampholyte » 26 Fév 2013, 14:46
Oui c'est exactement la même !
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 26 Fév 2013, 15:03
par Anthony666 » 26 Fév 2013, 15:03
Sa reste toujours un mystère pour moi , je n'arrive pas à trouver les responses aux questions à partir de la 2)a)

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 26 Fév 2013, 15:06
par ampholyte » 26 Fév 2013, 15:06
On sait que A1(-1; 0) donc pour trouver T1 on applique la formule :
T1 = f'(-1)(x - (-1)) + 0
Il ne te reste plus qu'à calculer f'(-1) pour trouver T1
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 26 Fév 2013, 15:14
par Anthony666 » 26 Fév 2013, 15:14
D'accord mais pourquoi on trouve -1 au A1(-1;0) parce que dans mes résultats y a jamais de -1

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 26 Fév 2013, 15:16
par ampholyte » 26 Fév 2013, 15:16
Anthony666 a écrit:2)a) A1(-1,0)
A2(3,0)
A la question 2)b) je suis coincé
C'est toi qui a écrit ça ...
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 26 Fév 2013, 15:17
par Anthony666 » 26 Fév 2013, 15:17
je trouve T1 = -4x -4
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 26 Fév 2013, 15:18
par Anthony666 » 26 Fév 2013, 15:18
C'est quelqu'un qui m'avait aider mais j'ai pas compris où il a trouvé ce -1
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 26 Fév 2013, 15:19
par Anthony666 » 26 Fév 2013, 15:19
T2 je trouve T2 = 4x-12

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 26 Fév 2013, 15:21
par ampholyte » 26 Fév 2013, 15:21
Déterminer les coordonnées des points A1 et A2 où la parabole P coupe l'axe des abscisses
Pour trouver A1 et A2 il suffit de résoudre f(x) = 0.
En résolvant on trouve x = -1 et x = 3 d'où
A1(-1; 0) et A2(3; 0)
On a : f(x)= x²-2x-3 donc f'(x) = 2x - 2
f'(-1) = -2 - 2 = -4
f'(3) = 6 - 2 = 4
T1 = -4(x + 1) = -4x - 4
T2 = 4(x - 3) = 4x - 12
Tes résultats sont donc justes !
-
Anthony666
- Membre Naturel
- Messages: 13
- Enregistré le: 25 Fév 2013, 19:34
-
 par Anthony666 » 26 Fév 2013, 15:22
par Anthony666 » 26 Fév 2013, 15:22
Enfin ensuite pour tracer T1 et T2 comment je procède ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
