Bonjour, je me sens coupable de ne pas pouvoir aider mon fils sur la dérivation etant donné que c'est loin derrière moi. Il me demande:
-Démontrer que , si la fonction g est définie pour tout réel x différent de -3 par g(x)= -3/x+3 , alors, pour tout
réel a,g est dérivable et g' ( a)= 3/ (a + 3)²
- Peut - on déterminer d'autres fonctions admettant , pour tout réel a différent de -3, un nombre dérivé égal à 3/ (a+3)²
Merci de vos réponses d'avance
Dérivation point de vue local
6 messages
- Page 1 sur 1
Re: Dérivation point de vue local
Voici de quoi vous dépanner
https://www.maths-et-tiques.fr/telech/F ... derive.pdf
(passez les démonstrations dans un premier temps)
g=-3.h pour h la fonction définie par h(x)=1/(x+3)
ATTENTION AUX PARENTHÈSES dans g(x)
donc g'=-3.h'
puis voir (1/u)' dans le document
deuxième question : toutes les fonctions f définies par f=g+C où C est une constante
Proposez vos essais, bon courage
https://www.maths-et-tiques.fr/telech/F ... derive.pdf
(passez les démonstrations dans un premier temps)
g=-3.h pour h la fonction définie par h(x)=1/(x+3)
ATTENTION AUX PARENTHÈSES dans g(x)
donc g'=-3.h'
puis voir (1/u)' dans le document
deuxième question : toutes les fonctions f définies par f=g+C où C est une constante
Proposez vos essais, bon courage
Re: Dérivation point de vue local
Bonjour,
pour la première question, il s'agit ni plus ni moins que l'application d'une formule du cours : si u est une fonction dérivable alors la dérivée de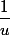 est... (il faut ici faire l'effort d'aller rechercher ce qu'on est censé avoir appris et qui se trouve dans le cours).
est... (il faut ici faire l'effort d'aller rechercher ce qu'on est censé avoir appris et qui se trouve dans le cours).
Pour la seconde question, on considère une autre fonction h vérifiant cette égalité, que peut-on alors dire de g'-h' pour tout réel distinct de 3 ? On utilise ensuite simplement le fait que g'-h'=(g-h)' et on sait alors que la fonction g-h a une propriété intéressante car son taux de variation est...
pour la première question, il s'agit ni plus ni moins que l'application d'une formule du cours : si u est une fonction dérivable alors la dérivée de
Pour la seconde question, on considère une autre fonction h vérifiant cette égalité, que peut-on alors dire de g'-h' pour tout réel distinct de 3 ? On utilise ensuite simplement le fait que g'-h'=(g-h)' et on sait alors que la fonction g-h a une propriété intéressante car son taux de variation est...
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dérivation point de vue local
Merci , mais j'ai pas compris la deuxième question....
Vous pouvez m'en dire plus s'il vous plait
Vous pouvez m'en dire plus s'il vous plait
Re: Dérivation point de vue local
Pour la seconde question, on demande "peut-on déterminer d'autres fonctions vérifiant...".
Appelons h une telle autre fonction. Alors on a
=h'(a))
Ce qui revient à écrire (je vous laisse compléter les pointillés)
-h'(a)=\cdots)
Or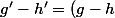') on a donc, en posant
on a donc, en posant 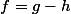
=\cdots)
Commencez par répondre à cette question : qu'y a-t-il à la place des "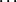 " ?
" ?
Appelons h une telle autre fonction. Alors on a
Ce qui revient à écrire (je vous laisse compléter les pointillés)
Or
Commencez par répondre à cette question : qu'y a-t-il à la place des "
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dérivation point de vue local
Pour la deuxième question, on ne vous demande pas de déterminer toutes les fonctions ayant la même dérivée que g (ce qui serait du programme de terminale, cet exercice ma parait être posé en première) mais seulement de montrer qu'il y en a.
Je vous avais donné la réponse lors de mon premier message : il ne reste qu'à justifier cette réponse :
si g et h sont deux fonctions dérivables sur un intervalle I, et f=g+h
f'=g'+h'
la dérivée d'une fonction constante est ...
(tout ceci est dans le document indiqué lors de ma première réponse, au cas très envisageable où le cours serait inexploitable, voire inexistant)
Bon courage
Je vous avais donné la réponse lors de mon premier message : il ne reste qu'à justifier cette réponse :
si g et h sont deux fonctions dérivables sur un intervalle I, et f=g+h
f'=g'+h'
la dérivée d'une fonction constante est ...
(tout ceci est dans le document indiqué lors de ma première réponse, au cas très envisageable où le cours serait inexploitable, voire inexistant)
Bon courage
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
