Dérivation de fonction

par **HERCOLUBUS** » 22 Nov 2011, 03:25

Si

Que vaut

et

?

par **HERCOLUBUS** » 22 Nov 2011, 23:08

Laissez-moi savoir vos démarches ! :D

par **Dlzlogic** » 22 Nov 2011, 23:23

Bonsoir,
La question posée est l'application stricte du cours. Il n'y a rien à comprendre, rien à expliques, juste à faire, sans se tromper.
Qu'attendez-vous de nous ?

par **HERCOLUBUS** » 27 Nov 2011, 20:07

Dlzlogic a écrit:Bonsoir,
La question posée est l'application stricte du cours. Il n'y a rien à comprendre, rien à expliques, juste à faire, sans se tromper.
Qu'attendez-vous de nous ?

Je veux simplement vérifier mes réponses, pour voir si j'ai compris!

par **Dlzlogic** » 27 Nov 2011, 20:18

Ca c'est le boulot du prof. On ne veut pas être accusées de concurrence déloyale.

par **HERCOLUBUS** » 12 Jan 2012, 23:21

Dlzlogic a écrit:Ca c'est le boulot du prof. On ne veut pas être accusées de concurrence déloyale.

Tes commentaires sont désobligeants, dans une optique constructive et cordiale je voudrais savoir comment me débrouiller pour dériver cette fonction.

Pour trouver la dérivé de

, j'ai utilisé la forme

Ce qui m'a donner comme résultat

Suis-je dans la bonne direction pour trouver la dérivée seconde ???
A partir de ce point devrai-je utiliser la forme

par **Jota Be** » 12 Jan 2012, 23:39

HERCOLUBUS a écrit:Tes commentaires sont désobligeants, dans une optique constructive et cordiale je voudrais savoir comment me débrouiller pour dériver cette fonction.

Pour trouver la dérivé de , j'ai utilisé la forme

Ce qui m'a donner comme résultat

Suis-je dans la bonne direction pour trouver la dérivée seconde ???
A partir de ce point devrai-je utiliser la forme

je crois que tu t'es trompé(e) dans le calcul de f'(x).
Je te conseille d'appliquer le cas particulier de dérivation des fonctions composées de forme

.
La dérivée est donc

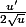
. Cela t'aidera plus à trouver la réponse facilement.
Au fait, la dérivée de

est

par **HERCOLUBUS** » 13 Jan 2012, 00:23

Jota Be a écrit:je crois que tu t'es trompé(e) dans le calcul de f'(x).
Je te conseille d'appliquer le cas particulier de dérivation des fonctions composées de forme .
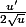
La dérivée est donc . Cela t'aidera plus à trouver la réponse facilement.
Au fait, la dérivée de est

Je crois avoir calculé juste, en calculant avec

,
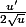
J'arrive a

que j'ai simplifié a

Qu'en penses-tu Jota Be?

Et qu'en pensez-vous (autres membres du forum) ?

par **Sylviel** » 13 Jan 2012, 00:36

C'est juste mais on peut simplifier...

par **HERCOLUBUS** » 13 Jan 2012, 00:43

Sylviel a écrit:C'est juste mais on peut simplifier...

De quelle manière !!??

par **Sylviel** » 13 Jan 2012, 00:45

si tu connais les puissances fractionnaires c'est assez facile... Sinon

par **HERCOLUBUS** » 13 Jan 2012, 00:50

Sylviel a écrit:si tu connais les puissances fractionnaires c'est assez facile... Sinon

Ouf ! Ça dépasse mon niveau de raisonnement actuel.
Je pensais qu'on pouvait avoir cette dérivé simplifié sous la forme f'(x)= ...

par **Dinozzo13** » 13 Jan 2012, 04:00

HERCOLUBUS a écrit:Je crois avoir calculé juste, en calculant avec ,
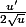
J'arrive a
que j'ai simplifié a

Qu'en penses-tu Jota Be?

Et qu'en pensez-vous (autres membres du forum) ?

En te servant du fait que

et que

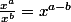
tu as :

:+++:

par **Carpate** » 13 Jan 2012, 11:55

HERCOLUBUS a écrit:Ouf ! Ça dépasse mon niveau de raisonnement actuel.
Je pensais qu'on pouvait avoir cette dérivé simplifié sous la forme f'(x)= ...

Nul besoin de simplifier ...

De la forme

avec

-->

par **HERCOLUBUS** » 13 Jan 2012, 20:02

:id: Ahhh yeah ! :lol3:

Vos interventions mon grandement aidées !
La dérivé seconde de

est donc

:zen:

Merci à tous !

Dérivation de fonction

Dérivation de fonction

Qui est en ligne