Dérivabilité en 0

par **Anonyme** » 20 Sep 2005, 22:19

Salut tout le monde,

J'ai un peu du mal pour ce qui suit, merci de votre aide

Etudier la dérivabilité en 0 de x--->(x-2)*racine(x)
Merci de bien expliquer

Merci de votre aide

par **S@m** » 20 Sep 2005, 22:24

Salut!
Quel est ton niveau? As-tu vu la dérivée d'une fonction f(x) notée f'(x) ou simplement l'accroissement moyen?

par **Anonyme** » 20 Sep 2005, 22:42

début de la terminale S,

en fait, je crois qu'il faut utiliser la définition du nb dérivée mais je n'arrive pas à lever l'indéterlination meme avec ca

par **S@m** » 20 Sep 2005, 22:46

Tu parles biend e la fonction qui a x associe

par **Anonyme** » 20 Sep 2005, 22:51

bien sur, je parle de cette fonction

par **S@m** » 20 Sep 2005, 22:56

Heu il est assez tard et je sais pas vraiment si ce que je dis là est juste, mais si tu calcules la limite en 0, tu trouves 0 et cette limite est bien égale à f(0) aussi égale a 0. Donc f(x) est dérivable en 0....

par **Nicolas_75** » 21 Sep 2005, 05:14

"en fait, je crois qu'il faut utiliser la définition du nb dérivée mais je n'arrive pas à lever l'indéterlination meme avec ca"

Je ne vois pourtant pas où est la difficulté. Il n'y a pas d'indétermination.

quand

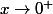
(en effet le numérateur tend vers -

et le dénominateur vers

)

Nicolas

par **S@m** » 21 Sep 2005, 05:48

J'ai enlevé mon précédent message, qui comportait certainement des erreurs vu l'heure tardive et ma fatigue...Par contre, je suis certaine en effet qu'il n' y a pas d'indetermination ... :++:

par **Anonyme** » 21 Sep 2005, 17:46

Re

En fait j'arrive facilement à faire ca mais quand j'ai -2 / 0+, je dis -oo ce qui est faux, puisque la limite (x-2)racine de( x) quand x tend vers 0 vaut 0.

par **Nicolas_75** » 21 Sep 2005, 18:08

Pourquoi est-ce faux ?
Sous la forme

qui semble te poser problème, le numérateur et le dénominateur tendent vers 0. C'est une forme indéterminée. On ne peut rien dire de leur rapport (sous cette forme).

par **Anonyme** » 21 Sep 2005, 20:58

re -

Pour répondre je fais ca :

et je finis en disant :

Or la limite de f(x) quand x tend vers 0 vaut 0,
Alors je répètes ma question pourquoi mon raisonnement est faut (je sais que c'est faut lol mais je ne comprends toujours mon erreur)?

Merci de bien expliquer svp

par **Alpha** » 21 Sep 2005, 21:53

Salut, Olep,

ce que tu as montré, ce n'est pas que la limite de f(x) quand x tend vers 0 est - l'infini!

Tout est juste dans ce que tu as fait, sauf la dernière ligne!

La conclusion, c'est que la limite de [f(x) - f(0)] / [x-0], quand x tends vers 0, est - l'infini, ce qui est très différent de ce que tu as écrit dans ta dernière ligne.

Pour dire les choses de façon encore plus détaillée :

[f(x) - f(0)] / [x-0] est différent de f(x) !

Cordialement

par **Ismail** » 21 Sep 2005, 21:59

Salut
je crois que tu melange entre la limite de f en 0+ et la derivabilité de f en 0+.
et c la derivabilité qu'on demande dans ton enoncé

par **Nicolas_75** » 22 Sep 2005, 03:33

Pour en rajouter une couche :
On montre que :
a)

b)

Il n'y a aucune contradiction entre ces 2 résultats.

par **Anonyme** » 22 Sep 2005, 07:46

Re_

quand j'ai :

dans ma tête ca devient :

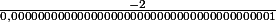
, c'est pourquoi je dis que c'est -OO

par **Nicolas_75** » 22 Sep 2005, 08:00

Tu es en train de dire que :

Nous sommes d'accord.
Où est le problème ?

par **Anonyme** » 22 Sep 2005, 08:31

Re Nicolas.

si c'est -OO il n'y a aucun problème mais si c'est 0 il y a un grand problème lol

par **Nicolas_75** » 22 Sep 2005, 08:39

Olep, je suis perdu dans tes questions.
On a deux choses différentes :

a)

b)

Où est le problème ?

Dérivabilité en 0

Dérivabilité en 0

Qui est en ligne