Dérivabilité en un point

[Bertrand Hamant]

Bonjour je dois étudier la dérivabilité d'une fonction en un point particulier

La fonction est définie sur R par f(0) = 0 et pour tout réel x non nul

f(x) = x².cos 1/x

f est elle dérivable en 0

j'ai fait f(x) - f(0) / x - 0 = x.cos(1/x)

et lim de x.cos(1/x) = 0 + ou 0 - par conséquent f(x) n'est pas dérivable en 0

calculer sa dérivé

f'(x) = 2x cos(1/x) + x².cos(1/x).(-1/x²)

Merci de confirmer

puis f(x) = V(x^3)/ V(x-1) définie sur [0 ; 1 [

est-elle dérivable en 0 on trouve en calculant le taux d'accroissement


V(x^3)/ V(x-1) / x = V ( x / 1 - x )

et lim de V ( x / 1 - x ) = 0 par conséquent f(x) est dérivable en 0 est ce correcte ??

merci de confirmer

[Nicolas_75]

Je ne comprends pas ton :
"j'ai fait f(x) - f(0) / x - 0 = x.cos(1/x)
et lim de x.cos(1/x) = 0 + ou 0 - par conséquent f(x) n'est pas dérivable en 0
"

-x =0, x.cos(1/x)->0
Donc la fonction est dérivable en 0, de nombre dérivé 0.

[Bertrand Hamant]

bah sur R x peut tendre vers 0+ ou 0-, non ?

[becirj]

Première fonction

Puisque tu as trouvé que la limite du taux d'accroissement en 0 était une limite finie , cela prouve que f est dérivable en 0 et f'(0)=0
Le calcul de f' est faux : la dérivée de la fonction cos est le fonction -sin

Deuxième fonction

Il doit y avoir une erreur, la fonction n'est définie que sur [1,+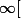 (j'ai supposé que V signifie racine}

[Nicolas_75]

Bertrand Hamant >
Bah et alors ?
0+ et 0-, cela reste 0 !
f telle que f(x)=x tend vers 0- pour x négatif et tend vers 0+ pour x positif.
Et elle est continue, non ?