Dérivabilité à gauche et à droite.

par **Jjl** » 26 Mai 2015, 16:02

paquito a écrit:C'est l'exercice le plus con que j'ai vu sur ce site!!! toute fonction polynôme est dérivable partout!!
Et, n'en déplaise à zygo, tu peut même écrire:

(3x^2+4x-5)'=6x+4 (Si Laurent Schwartz l'autorise....) et f'(3)=22. Point final.

L'exo le plus con à disparu t'inquiète.

par **zygomatique** » 26 Mai 2015, 16:18

Jjl a écrit:L'exo le plus con à disparu t'inquiète.

c'est dommage car il explique toute la discussion ....

celle-ci n'ayant d'autre intérêt que de te faire avancer dans la bonne direction .... ainsi que d'autres .... s'ils ont l'énoncé ....

:lol3:

par **Jjl** » 26 Mai 2015, 17:36

zygomatique a écrit:c'est dommage car il explique toute la discussion ....

celle-ci n'ayant d'autre intérêt que de te faire avancer dans la bonne direction .... ainsi que d'autres .... s'ils ont l'énoncé ....

:lol3:

Pas faux,mais jlai plu, Jv voir si jpeu le remettre...

par **paquito** » 26 Mai 2015, 17:53

On peut peut être trouver plus con!!

par **zygomatique** » 26 Mai 2015, 18:15

facile (et en rapport avec ton lien) (et qu'on peut surement proposer à certains Term S)

vérifier avec la calculatrice que 6/3 = 2 (c'est du vécu de la part d'une TS)

écrire un algorithme qui calcule 6 divisé par 3 !!!

:ptdr: :ptdr:

par **Jjl** » 26 Mai 2015, 19:42

paquito a écrit:On peut peut être trouver plus con!!

Tu parles de,lexo ou de moi?
Si c moi,oui... ya bcp plus bête et infiniment plus malin.

par **paquito** » 26 Mai 2015, 20:01

Jjl a écrit:Tu parles de,lexo ou de moi?
Si c moi,oui... ya bcp plus bête et infiniment plus malin.

comme exo, bien sûr; :lol3:

par **Jjl** » 26 Mai 2015, 20:12

paquito a écrit:comme exo, bien sûr; :lol3:

Ouf,je me serai senti vexé

par **Pseuda** » 26 Mai 2015, 21:14

C'était un exercice où il fallait repartir de la définition du nombre dérivé d'une fonction en un point. La fonction était une fonction polynôme, et on part du principe dans cet exercice qu'on ne sait rien sur les dérivées (à part la définition) et sur les fonctions polynômes.

par **Pseuda** » 28 Mai 2015, 18:51

mathelot a écrit:théorème:

soit

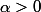
si f est continue sur
dérivable sur
si

alors
f est dérivable , à droite, en

Merci mathelot pour cette remarque. Sans le vouloir, tu as répondu à une question que je me pose depuis quelque temps. Je me demande quelle en est la démonstration. Aurais-tu un lien ou un aperçu ?

Merci d'avance.

par **zygomatique** » 28 Mai 2015, 18:55

c'est une définition qui se démontre de la même façon que la "dérivée normale" ... sauf qu'il n'y a pas de x < x_0

....

par **paquito** » 28 Mai 2015, 20:00

C'est surtout dû au fait que si f' a une limite à droite ou à gauche en x_0, le taux de variation a la même limite (accroissements finis)!!

Dérivabilité à gauche et à droite.

Qui est en ligne