Dépendance linéaire des vecteurs

[Skaler]

Bonjour,

une question concernant la dépendance linéaire des vecteurs :

La définition est la suivante :

"k vecteurs u1, u2, ....., uk sont linéaires dépendants, si b1*u1 + b2*u2 +...+ bk*bk = 0, mais tous les bj = 0"

Dans cette définition il me manque cependant l'ensemble dans lequel se trouve les produits b. N ? ou R ?

Merci

[Cryptocatron-11]

Ils appartiennent au corps K qui peut être R ou C

[Skaler]

Merci!

Bonne journée

[Skaler]

Pendant que j'y suis, une autre question me perturbe :

Quelque part dans ma théorie il est écrit :

- Chaque base de se compose de n vecteurs.
- n vecteurs linéaires indépendants dans l'ensemble constituent une base de .

Cependant, à l'exercice suivant :

Déterminer une base pour le sous-ensemble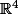 W1={x / x1+2x2-x3=0}

la réponse m'est donnée :
"
Comme les vecteurs :
sont linéaires indépendants, ils présentent une base pour W1."


Ma question enfin est la suivante, il n'y a ici que 3 vecteurs alors que ma théorie (si je la comprend bien) me dit que pour un domaine je dois avoir n vecteurs, donc ici 4 ! Non ?

Merci

[MacManus]

Bonjour,

Tu le dis toi-même, ces vecteurs forment une base pour W1, qui est un sous-espace de R4 de dimension 3.

[Skaler]

Bonjour,

Tu le dis toi-même, ces vecteurs forment une base pour W1, qui est un sous-espace de R4 de dimension 3.

C'est juste, merci. Tout à fait logique!

Dernière question :

toujours dans le chapitre des matrices et des vecteurs, pourquoi

rg(B) = 1, et non 0 ?



Puisque,


mais aussi

[MacManus]

Ta matrice ne peut pas être de rang 0 sinon ce serait la matrice nulle.
Les deux colonnes (ou deux lignes) de ta matrice B sont linéairement dépendantes, ta matrice B est donc de rang 1.

Une façon de déterminer le rang d'une matrice, est de déterminer la dimension du sous-espace vectoriel engendré par les vecteurs lignes (ou colonnes).

Pour B, utiliser le vecteur ligne (2,1) suffit. On peut chercher à résoudre, pour tout X=(x,y), le système BX=0. Ce qui donne 2x+y=0 qui est le sous-espace vectoriel engendré par x
Ce sous-espace est bien de dimension 1

[Skaler]

Ta matrice ne peut pas être de rang 0 sinon ce serait la matrice nulle.
Les deux colonnes (ou deux lignes) de ta matrice B sont linéairement dépendantes, ta matrice B est donc de rang 1.

Une façon de déterminer le rang d'une matrice, est de déterminer la dimension du sous-espace vectoriel engendré par les vecteurs lignes (ou colonnes).

Pour B, utiliser le vecteur ligne (2,1) suffit. On peut chercher à résoudre, pour tout X=(x,y), le système BX=0. Ce qui donne 2x+y=0 qui est le sous-espace vectoriel engendré par x
Ce sous-espace est bien de dimension 1

Merci !

Bonne journée