Dénombrement TS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Huit
- Membre Relatif
- Messages: 137
- Enregistré le: 10 Nov 2005, 20:39
-
 par Huit » 01 Avr 2006, 09:23
par Huit » 01 Avr 2006, 09:23
Bonjour à tous !
Voilà je commence un dm mais je bute sur la dernière question de la première partie d'un exo ! Ca serait sympa de me filer un coup de pouce !
On considère les sommes :
 + \(100\\3\) +\(100\\6\) +........+\(100\\99\))
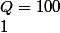 + \(100\\4\) +\(100\\7\) +........+\(100\\100\))
 + \(100\\5\) +\(100\\8\) +........+\(100\\98\))
1. Calculer P+Q+R
Je trouve 2^100
2. On pose
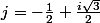
Calculer j^2 et établir les relations
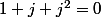
et
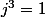
Tout cela est fait, on trouve
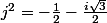
3.a) Calculer
^{100})
On trouve
^{100}=j^2)
b) En déduire que P+

Q+

R=

Ca j'ai aussi fait...
4. Déduire de ce qui précède les valeurs de P, Q et R.
Alors là je bloque... 3 inconnu, 2 équations ?? j'ai essayé de faire une autre équation en en multipliant par j mais je suis pas convaincu... Si quelqu'un pouvait m'aider ça me sauverais la vie !
Merci d'avance !
-
Huit
- Membre Relatif
- Messages: 137
- Enregistré le: 10 Nov 2005, 20:39
-
 par Huit » 01 Avr 2006, 11:11
par Huit » 01 Avr 2006, 11:11
Je suis vraiment bloqué et dans l'incapacité de poursuivre l'exercice...
Si quelqu'un n'a ne serait-ce qu'une intuition qu'il m'en fasse part s'il vous plait...
-
tigri
- Membre Rationnel
- Messages: 845
- Enregistré le: 15 Déc 2005, 22:28
-
 par tigri » 01 Avr 2006, 11:22
par tigri » 01 Avr 2006, 11:22
bonjour
je suis surprise que , au 2), on demande j=3 ??? vu que j=-1/2 +i (rac3)/2
-
Huit
- Membre Relatif
- Messages: 137
- Enregistré le: 10 Nov 2005, 20:39
-
 par Huit » 01 Avr 2006, 11:26
par Huit » 01 Avr 2006, 11:26
Désolé, il s'agit d'une erreur de frappe de ma part,
on demande de démontrer que
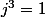
merci de me prêter attention !
-
tigri
- Membre Rationnel
- Messages: 845
- Enregistré le: 15 Déc 2005, 22:28
-
 par tigri » 01 Avr 2006, 11:33
par tigri » 01 Avr 2006, 11:33
bon, au début aussi, les sommes doivent s'appeler P,Q, R, mais... on avait compris
le reste est juste, mais moi non plus, je n'ai pas trouvé... encore... comment aboutir aux valeurs de P,Q,R
ce j^3=1 doit bien servir qqpart, mais en multipliant par j une des relations, on en obtient une autre équivalente, donc çà n'avance pas...
-
Huit
- Membre Relatif
- Messages: 137
- Enregistré le: 10 Nov 2005, 20:39
-
 par Huit » 01 Avr 2006, 11:40
par Huit » 01 Avr 2006, 11:40
Je vais tacher d'utiliser ce

Merci tout de même d'avoir pris du temps pour moi

-
tigri
- Membre Rationnel
- Messages: 845
- Enregistré le: 15 Déc 2005, 22:28
-
 par tigri » 01 Avr 2006, 11:42
par tigri » 01 Avr 2006, 11:42
de rien; c'est intéressant, j'aimerais bien trouver... ou connaître la solution de quelqu'un !
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 01 Avr 2006, 11:42
par Mikou » 01 Avr 2006, 11:42
non, regardez il ya une relation simple entre Q et R
nb :
 = \(100\\99\) de meme \(100\\4\)=\(100\\96\))
voila ...
-
Huit
- Membre Relatif
- Messages: 137
- Enregistré le: 10 Nov 2005, 20:39
-
 par Huit » 01 Avr 2006, 11:58
par Huit » 01 Avr 2006, 11:58
erf lol déçu de pas l'avoir vu moi même !
Merci beaucoup !
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 01 Avr 2006, 12:01
par Mikou » 01 Avr 2006, 12:01
ce n'est rien, dailleurs tigri lui non plus n'avait pas non plus immediatement vu l'astuce :++:
 par Sasuke_Uchina » 01 Avr 2006, 12:42
par Sasuke_Uchina » 01 Avr 2006, 12:42
On pourrait calculer
^{100}=j)
donc

d'ou le systeme



pour le résoudre , on pense à Euler.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 91 invités
