Démontrer et utiliser l'IAG - Polynômes symétriques
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 19 Oct 2009, 10:58
par Timothé Lefebvre » 19 Oct 2009, 10:58
Salut tout le monde

Aujourd'hui je vous propose un exo assez sympa qui met en jeu la démonstration de l'Inégalité Arithmético-Géométrique (IAG) que vous connaissez peut-être.
Énoncé :On pose x,y et z des réels positifs ou nuls tels que leur somme égale 1.
Montrer que :
[center]

[left]On se servira de l'IAG (aussi appelée inégalité de la moyenne) que l'on démontrera au cours du raisonnement.
Rappel de l'énoncé de l'IAG :Soient

,

, ...,

des réels positifs, alors :
[center]

[left]Bon courage et bonne fin de journée !
Tim
[/left]
[/center]
[/left]
[/center]
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Oct 2009, 11:45
par Nightmare » 19 Oct 2009, 11:45
Salut,
j'ai trouvé sans IAG en voyant la somme comme une fonction de z :
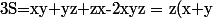+xy(1-2z)=z(1-z)+xy(1-2z))
Or,
^{2})
et on en déduit que
+\frac{1}{4}(1-z)^{2}(1-2z))
En posant
=z(1-z)+\frac{1}{4}(1-z)^{2}(1-2z))
on remarque que
=\frac{7}{27})
. Reste donc à montrer que S(z) atteint son maximum en 1/3.
Pour ça il faut remarquer que x, y et z ne peuvent être tous les 3 supérieurs à 1/3. On peut donc supposer quitte à permuter que z est inférieur à 1/3. L'étude de S(z) sur [0,1/3] (dérivée + tableau de variation) donne rapidement pour tout z, S(z) < S(1/3) CQFD.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 19 Oct 2009, 15:19
par Timothé Lefebvre » 19 Oct 2009, 15:19
Salut à toi,
je ne l'avais pas vu comme ça tiens !
Je passe l'inégalité avec 0 (elle est simple à démontrer).
Pour l'inégalité de droite j'ai noté que les éléments formaient des polynômes symétriques (d'où le nom de l'exercice).
Je pose donc le polynôme : P(n)=(n-x)(n-y)(n-z).
Si je place ce polynôme dans l'inégalité je tombe alors sur 2(P(1/2)+1/8)

7/27 que je prouve avec l'IAG.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Oct 2009, 15:31
par Nightmare » 19 Oct 2009, 15:31
Je ne comprends pas ce que tu entends par "j'ai noté que les éléments formaient des polynômes symétriques" !
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 19 Oct 2009, 15:33
par Timothé Lefebvre » 19 Oct 2009, 15:33
Eh bien les éléments de l'inégalité sont des polynômes symétriques élémentaires, non ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Oct 2009, 15:37
par Nightmare » 19 Oct 2009, 15:37
Ah, tu veux dire que xy+yz+zx-4xyz est un polynôme symétrique ok. D'accord pour ta preuve.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 19 Oct 2009, 15:40
par Timothé Lefebvre » 19 Oct 2009, 15:40
Oui, désolé si je n'ai pas été clair.
D'autres avaient-ils des preuves différentes des nôtres ?
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 21 Oct 2009, 15:36
par Zweig » 21 Oct 2009, 15:36
On pose
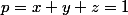
,
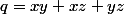
,
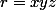
L'inégalité à démontrer se réécrit alors :
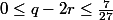
L'inégalité de Schur s'énonce comme suit :
(x-z)+y^{t}(y-x)(y-z)+z^{t}(z-x)(z-y)\geq0)
pour tout réel

et réels positifs

,

,

Pour
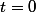
nous avons :
(x-z)+y^0(y-x)(y-z)+z^0(z-x)(z-y)\geq0\Leftrightarrow pq-9r\geq0)
Pour
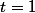
nous avons :
(x-z)+y^{1}(y-x)(y-z)+z^{1}(z-x)(z-y)\geq0\Leftrightarrow p^{3}-4pq+9r\geq0)
De ces deux inégalités on en déduis un encadrement pour

et

:
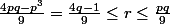
(1)
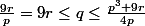
(2)
De (2) nous avons
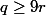
et puisque
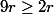
alors par transitivité,
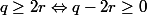
L'inégalité à démontrer se réécrit aussi
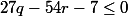
De (1) nous avons
-7=3q-1)
Or il est bien connu que
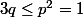
d'où
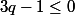
et ainsi par transitivité,
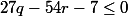
Ainsi nous avons prouvé que
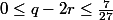
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Oct 2009, 14:25
par Timothé Lefebvre » 23 Oct 2009, 14:25
Sympa Zweig

En ce qui concerne la démo de l'IAG je propose de faire une simple étude de cas.
Si l'un des

est nul (on a

) alors le résultat est évident.
Si ce n'est pas le cas alors il suffit de poser

,
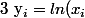)
.
Dans ce dernier cas, l'inégalité devient une simple conséquence du fait de la convexité de l'exponentielle (on aura au préalable réécrit l'inégalité sous cette forme pour parvenir à ça).
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 23 Oct 2009, 15:10
par Zweig » 23 Oct 2009, 15:10
Question subsidiaire : Démontrer l'IAG par récurrence :zen:.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Oct 2009, 15:41
par Timothé Lefebvre » 23 Oct 2009, 15:41
Lol, bonne idée tiens ^^
Un volontaire ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Oct 2009, 18:31
par Nightmare » 23 Oct 2009, 18:31
Pour n=2 c'est Cauchy-Schwartz et par identité remarquable et récurrence on montre que c'est vrai pour tous les 2^n, on conclut pour n quelconque en prenant la moyenne arithmétique des n premiers (en gros).
Une autre méthode consiste à examiner les extrema de
_{i\le n} \to x_{1}x_{2}...x_{n})
sous la contrainte
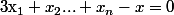
avec x quelconque positif et d'appliquer le théorème des extrema liés.
Bref, encore un énoncé avec plein de jolies méthodes.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Oct 2009, 20:14
par Timothé Lefebvre » 23 Oct 2009, 20:14
En fait je crois qu'on peut aussi appliquer l'inégalité du réordonnement pour démontrer l'IAG (il me semble l'avoir lu quelque part).
Cependant, si mes souvenirs sont bons on a besoin de la méthode de Cauchy dont tu parles Nightmare pour traiter le cas d'égalité.
Un exemple intéressant avec l'IAG : comment relier la moyenne harmonique à la moyenne géométrique de n réels strictement positifs ?
Après il me semble aussi qu'on peut s'intéresser à l'inégalité de Chebychev dans le même rayon.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 23 Oct 2009, 20:21
par Nightmare » 23 Oct 2009, 20:21
Qu'appelles-tu méthode de Cauchy?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 23 Oct 2009, 20:25
par Timothé Lefebvre » 23 Oct 2009, 20:25
Nightmare a écrit:Pour n=2 c'est Cauchy-Schwartz et par identité remarquable et récurrence on montre que c'est vrai pour tous les 2^n, on conclut pour n quelconque en prenant la moyenne arithmétique des n premiers (en gros).
Exactement celle-là.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités

 ,
,  , ...,
, ...,  des réels positifs, alors :
des réels positifs, alors :

 7/27 que je prouve avec l'IAG.
7/27 que je prouve avec l'IAG.