Demontrer une propriété pas récurrence
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
annasonne
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Sep 2008, 18:54
-
 par annasonne » 15 Sep 2008, 18:58
par annasonne » 15 Sep 2008, 18:58
Bonjour/Bonsoir
J'aimerai un peu d'aide pour résoudre cet exercice
(Un) n N*
U1=U2=1
Un+2=Un+1+Un
Démontrer par récurrence:
1)U1²+U2²+...+Un²=Un*Un+1
2)Un=(1/Racine5)(((1+Racine5)/2)n-((1-Racine)/2)n)
1)Démontrer la propriété au rang U1:
U1²=U3²-U2²
Je vois pas trop comment trouver U3
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 15 Sep 2008, 19:06
par L.A. » 15 Sep 2008, 19:06
Bonsoir,
Pour 1), quelle est la forme de la propriété à démontrer pour le rang 1 ?
Pour 2), il s'agit de prouver que la formule donnée est bien celle de la suite de fibonacci définie par récurrence
-
annasonne
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Sep 2008, 18:54
-
 par annasonne » 15 Sep 2008, 19:25
par annasonne » 15 Sep 2008, 19:25
1) démontrer que U1²=U1*U2 Non?
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 15 Sep 2008, 20:00
par L.A. » 15 Sep 2008, 20:00
annasonne a écrit:1) démontrer que U1²=U1*U2 Non?
Oui, et comme on connait les valeurs qui interviennent ... :id:
L'initialisation terminée on passe à l'hérédité.
-
annasonne
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Sep 2008, 18:54
-
 par annasonne » 15 Sep 2008, 20:22
par annasonne » 15 Sep 2008, 20:22
pour voir si j'ai bien compris:
U1=1
or
^2=U_1*U_2=1*1=1)
Démontrer la prop au rang p:
=(U_p)^2)
=(U_p+1)^2)
a démontrer
heu ensuite là je vois pas
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 15 Sep 2008, 20:27
par L.A. » 15 Sep 2008, 20:27
Il n'es pas à montrer :
Un² = UnUn+1
mais
U1² + U2² + ... + Un² = UnUn+1
Enfin tu l'as dit toi même... :triste:
-
annasonne
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Sep 2008, 18:54
-
 par annasonne » 15 Sep 2008, 20:36
par annasonne » 15 Sep 2008, 20:36
ah oui exact :mur:
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 15 Sep 2008, 20:38
par L.A. » 15 Sep 2008, 20:38
Bon alors pour l'hérédité au rang n:
Quelle est la supposition ?
Que doit on démontrer à partir de là ?
-
annasonne
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Sep 2008, 18:54
-
 par annasonne » 15 Sep 2008, 20:42
par annasonne » 15 Sep 2008, 20:42
^2 + (U_2)^2 + ... + U^2_p+1 = U_(p+1)*U_(p+2))
mais je crois pas que c'est de là qu'on doit partir
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 15 Sep 2008, 20:45
par L.A. » 15 Sep 2008, 20:45
Non, c'est justement ce qu'on souhaite démontrer, en supposant que la prop. au rang inférieur (càd p) est vraie.
Je te repose la question du message précédent, qui appelle 2 parties de réponse.
-
annasonne
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Sep 2008, 18:54
-
 par annasonne » 15 Sep 2008, 20:56
par annasonne » 15 Sep 2008, 20:56
J'ai pas vraiment compris ce qui fallait faire en cours, alors j'ai essayais d'appliquer ce qu'on a fait...
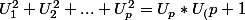)
+U^2_p+ U^2_(p+1)=U_p*U_(p+1) + U^2_(p+1))
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 15 Sep 2008, 21:00
par L.A. » 15 Sep 2008, 21:00
Reprenons l'hérédité alors.
Je suppose que la propriété au rang p :
U1² + ... + Up² = Up*Up+1
est vraie, et je doit montrer que la propriété au rang p+1 :
U1² + ... + Up² + Up+1² = Up+1*Up+2
est vraie aussi.
OK ?
-
annasonne
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Sep 2008, 18:54
-
 par annasonne » 15 Sep 2008, 21:05
par annasonne » 15 Sep 2008, 21:05
oui on s'arrête jusqu'au rang Un+1 au lieu de Un
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 15 Sep 2008, 21:07
par L.A. » 15 Sep 2008, 21:07
C'est grossomodo ça.
Donc on part de Sp = Up*Up+1
(j(ai posé Sp = somme des carrés de (Un) = U1²+...+Up²)
et on doit montrer à partir de là :
Sp+1 = Up+1*Up+2
Constatons que Sp+1 = Sp + Up+1²
Je te laisse finir...
-
annasonne
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Sep 2008, 18:54
-
 par annasonne » 15 Sep 2008, 21:14
par annasonne » 15 Sep 2008, 21:14
Ok je verrais ça demain matin, sinon j'aurai pas assez d'heure de sommeil merci en tout cas de donner de ton temps =)
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 15 Sep 2008, 21:15
par L.A. » 15 Sep 2008, 21:15
annasonne a écrit:Ok je verrais ça demain matin, sinon j'aurai pas assez d'heure de sommeil merci en tout cas de donner de ton temps =)
C'est un plaisir...
-
annasonne
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Sep 2008, 18:54
-
 par annasonne » 21 Sep 2008, 15:51
par annasonne » 21 Sep 2008, 15:51
Bonjour, je dois démontrer par récurrence que
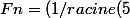)(((1+racine(5))/2)^n-((1-racine(5))/2)^n))
j'ai réussi à démontrer au rang 1 mais je ne vois pas du tout comment faire au rang P. Quelqu'un peut-il m'aider?
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 22 Sep 2008, 07:24
par L.A. » 22 Sep 2008, 07:24
Rebonjour.
Il faut donc vérifer que la formule Fn que tu proposes est bien celle de la suite de Fibonacci Un définie par récurrence.
Pour cela on doit vérifer que :
F0 = U0
F1 = U1
et pour tout n Fn+2 = Fn+1 + Fn
Mais ici on ne procède pas par récurrence. on montre directement la formule au rang n, sans supposer quelle est vraie au rang (n-1).
On part de Fn+1 + Fn, et on montre que c'est bien égal à Fn+2.
-
annasonne
- Membre Naturel
- Messages: 18
- Enregistré le: 15 Sep 2008, 18:54
-
 par annasonne » 22 Sep 2008, 17:58
par annasonne » 22 Sep 2008, 17:58
Peut -on dire???
=(\frac{1+\sqrt{5}}{2})^(P+1) (\frac{1+\sqrt{5}}{2})- (\frac{1-\sqrt{5}}{2})^(p+1)(\frac{1-\sqrt{5}}{2}))
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 23 Sep 2008, 07:39
par L.A. » 23 Sep 2008, 07:39
Ben presque.
ce que tu dis est vrai si p=n et sans oublier le 1/V5 devant.
Mais où veux-tu en venir ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
