Démontrer une inégalité

[garthalgar]

Bonjour,

Je bute un peu sur l'exercice suivant :

1) Calculez l'intégrale suivante I=

La primitive est (lnx)²/2 et je trouve donc I= (ln2)²/2

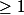
2) Montrez que pour tout réel x tel que x on a

C'est là que je ne vois pas trop comment m'y prendre...

[ampholyte]

Bonjour,

1) Je dirais plutôt que I = - (ln2)²/2

2) Essaye d'utiliser l'intégral sur l'ensemble pour voir ce que ça donne.
Tu peux déjà essayer de montrer un côté puis l'autre côté par la suite.

[Black Jack]

2)

avec x >= 1 montrer que x/(1+x²) <= 1/x

f(x) = x/(1+x²) - 1/x
f(x) = (x²-1-x²)/(x(1+x²))
f(x) = -1/(x(1+x²))

Pour x >= 1, on a donc f(x) < 0

--> x/(1+x²) - 1/x < 0
x/(1+x²) < 1/x
*****

g(x) = 1/(2x) - x/(1+x²)
...


:zen:

[garthalgar]

Bonjour,

1) Je dirais plutôt que I = - (ln2)²/2

Je me suis trompé dans la notation de mon intégrale en fait, j'édite.