Démontrer une formule
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par Mllemariion11 » 03 Nov 2013, 19:54
par Mllemariion11 » 03 Nov 2013, 19:54
Démontrer que :
Pour tout nE IN 1*2 + 2*3 +...+ n*(n + 1) = n(n + 1)(n + 2)/3
Est ce que quelqu'un pourrait m'aider svp :we:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 03 Nov 2013, 20:16
par chan79 » 03 Nov 2013, 20:16
Mllemariion11 a écrit:Démontrer que :
Pour tout nE IN 1*2 + 2*3 +...+ n*(n + 1) = n(n + 1)(n + 2)/3
Est ce que quelqu'un pourrait m'aider svp :we:
salut
par récurrence si tu connais
sinon tu peux écrire
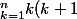=\bigsum_{k=1}^{n}k^2+ \bigsum_{k=1}^{n} k)
à condition de connaître ces deux sommes ...
 par Mllemariion11 » 03 Nov 2013, 20:18
par Mllemariion11 » 03 Nov 2013, 20:18
Merci , de m'avoir répondu :)
Je connais la récurrence mais je ne vois pas comment l'appliquer ici :/

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 03 Nov 2013, 20:20
par chan79 » 03 Nov 2013, 20:20
Mllemariion11 a écrit:Merci , de m'avoir répondu

Je connais la récurrence mais je ne vois pas comment l'appliquer ici :/
vérifie qua ta formule est vérifiée pour n=0
ensuite tu supposes que 1*2 + 2*3 +...+ n*(n + 1) = n(n + 1)(n + 2)/3
et tu calcules 1*2 + 2*3 +...+ n*(n + 1)+(n+1)(n+2)
 par Mllemariion11 » 03 Nov 2013, 20:37
par Mllemariion11 » 03 Nov 2013, 20:37
Je vérifie avec quelle formule ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 03 Nov 2013, 20:40
par chan79 » 03 Nov 2013, 20:40
Mllemariion11 a écrit:Je vérifie avec quelle formule ?
celle qu'on te demande de vérifier... remplace n par 0 et vois si c'est vrai
un petit coup d'oeil dans le cours sur la démonstration par récurrence serait bien, avant de s'attaquer aux exercices :zen:
 par Mllemariion11 » 03 Nov 2013, 20:45
par Mllemariion11 » 03 Nov 2013, 20:45
D'accord merci , je viens de voir qu'on avez fait une démonstration de ce genre , mais je pensais pas qu'on pouvait faire comme ça
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 94 invités
