Hello,
Je sollicite votre aide pour une correction d'exercice que je n'arrive pas à comprendre :mur: . Bon peut-être qu'avoir arrêté les maths durant 20 ans y est aussi pour quelque chose...
Bref :
Enoncé
on a f et g qui sont dérivables en a sur l'intervalle I. Montrer que fg est dérivable en a.
Correction
Considérant les accroissements moyens on a :
( (fg)(a+h) - (fg)(a) )/h = ( f(a+h)g(a+h) + f(a)g(a) )/h
jusque là tout va bien...
= ( [f(a+h)-f(a)]g(a+h) + f(a)[g(a+h)-g(a)] )/h
Là déjà, je comprends plus. Pour moi qqch du genre ab+dc est égal à (a-c)b + c(b+d) mais pas à (a-c)b + c(b-d). Et puis quand bien même, c'est quoi la méthode pour passer de ab+dc à (a-c)b + c(b-d) ?
= g(a) x ( f(a+h)-f(a) )/h + f(a) x ( g(a+h)-g(a) )/h
Le coup de grace... Comment g(a+h) peut-il se transformer en g(a) dans g(a) x ( f(a+h)-f(a) )/h ?
Effectivement, la dernière égalité montre bien que (fg)' = f'g + fg' en a. Mais je comprends pas toutes ces astuces de calcul :hum: . Si quelqu'un pouvait m'éclairer :cry2:
Gab.
Démontrer que fg est dérivable en a
7 messages
- Page 1 sur 1
En TEX c'est mieux...
Oups pardon, je viens de voir comment on utilise TEX. Donc je réécris la correction ci-dessus en TEX pour plus de lisibilité :
(a+h)-(fg)(a)}{h} = \frac {f(a+h)g(a+h)+f(a)g(a)}{h})
-f(a)]g(a+h) + f(a)[g(a+h)-g(a)]}{h})
-f(a)}{h}g(a) + f(a)\frac{g(a+h) - g(a)}{h})
Gab.
Gab.
Ok merci pour votre aide, je comprends mieux maintenant.
Ils ont donc mis un +f(a)g(a) à la place de -f(a)g(a) dans la première ligne. La deuxième ligne est juste car elle ne tient pas compte de cette erreur.
Donc du coup je comprends bien pourquoib+c(b-d))
Mais par contre je ne me rappelle pas avoir déjà vu une méthode pour transformer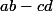 en
en  + c(b-d)) . Est-ce quelque chose à savoir ou bien une astuce à trouver sur le moment ? Bon enfin je tâcherai de m'en souvenir quand même.
. Est-ce quelque chose à savoir ou bien une astuce à trouver sur le moment ? Bon enfin je tâcherai de m'en souvenir quand même.
Enfin pour le g(a+h) qui mute en g(a), je dois me rappeler que h tend vers 0.
La correction fournie n'était donc pas sans défaut.
Encore merci :happy2:
--
Gab
Ils ont donc mis un +f(a)g(a) à la place de -f(a)g(a) dans la première ligne. La deuxième ligne est juste car elle ne tient pas compte de cette erreur.
Donc du coup je comprends bien pourquoi
Mais par contre je ne me rappelle pas avoir déjà vu une méthode pour transformer
Enfin pour le g(a+h) qui mute en g(a), je dois me rappeler que h tend vers 0.
La correction fournie n'était donc pas sans défaut.
Encore merci :happy2:
--
Gab
C'est une "astuce" dont on se sert quasi systématiquement lorsque on a une expression du styleGabrie1 a écrit:Mais par contre je ne me rappelle pas avoir déjà vu une méthode pour transformeren
. Est-ce quelque chose à savoir ou bien une astuce à trouver sur le moment ?
Donc par exemple, on utilise la même "astuce" pour montrer que le produit de deux fonctions continues est continue ou bien pour montrer que, si les suites Un et Vn tendent vers L et L' alors le produit UnVn tend vers LL'...
Donc c'est effectivement une "astuce classique"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
