Démontrer que deux angles sont égaux

par **Et0ile** » 14 Oct 2007, 07:57

Bonjour,

J'ai réussi toutes les questions, sauf la c) !

Pourriez-vous m'aider svp ?

Dans un triangle ABC rectangle en A, [AH] est la hauteur issue de A.
a) En écrivant de deux façons le cosinus de l'angle ABC, montrer que : BA²=BHxBC
b) Démontrer de manière analogue que : CA²=CHxCB
c)Expliquer pourquoi on a angle ABH = angle HAC

Merci d'avance

par **Fred_Sabonnères** » 14 Oct 2007, 08:23

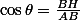
Mais aussi

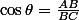
Tu en déduis la suite
A+

par **Et0ile** » 14 Oct 2007, 08:26

Fred_Sabonnères a écrit: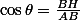
Mais aussi

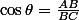
Tu en déduis la suite
A+

Mais en quoi cela peut-il aider à prouver que les angles sont égaux ? Car ça c'est la réponse de la question a), mais je ne vois pas comment l'exploiter pour la question c) ?

par **Et0ile** » 14 Oct 2007, 08:39

Jéjouille a écrit:Prouves qu'ils sont semblables

J'ai essayé, mais je n'ai pas su comment m'y prendre :triste:

par **Et0ile** » 14 Oct 2007, 08:45

Pour prouver qu'ils sont semblables, il faut connaitre minimum deux angles, et là, je sais qu'ils ont tous les deux 90°, mais je ne connais pas les autres angles.

par **Et0ile** » 14 Oct 2007, 08:50

Et on a pas encore vu les triangles semblables cette année... y'a pas une autre méthode ? :hein:

Démontrer que deux angles sont égaux

Démontrer que deux angles sont égaux

Qui est en ligne